Euler systems for number fields
Towards the end of 1980s, F. Thaine [a28] discovered a new method for investigating the class groups (cf. also Class field theory) of real Abelian extensions of 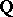 (cf. also Extension of a field). His method turned out to be the first step of a descent procedure introduced by V.A. Kolyvagin, shortly after Thaine's result. Kolyvagin used this procedure to investigate class groups of Abelian extensions of
(cf. also Extension of a field). His method turned out to be the first step of a descent procedure introduced by V.A. Kolyvagin, shortly after Thaine's result. Kolyvagin used this procedure to investigate class groups of Abelian extensions of 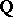 and Abelian extensions of quadratic fields [a10] (see also [a20]). In addition, Kolyvagin showed that this method extends to problems concerning Mordell–Weil groups and Tate–Shafarevich groups of modular elliptic curves over
and Abelian extensions of quadratic fields [a10] (see also [a20]). In addition, Kolyvagin showed that this method extends to problems concerning Mordell–Weil groups and Tate–Shafarevich groups of modular elliptic curves over 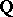 [a9], [a10] (cf. also Elliptic curve; Galois cohomology). The key idea of Kolyvagin's method is to construct a family of cohomology classes indexed by an infinite set of square-free integral ideals of the base field
[a9], [a10] (cf. also Elliptic curve; Galois cohomology). The key idea of Kolyvagin's method is to construct a family of cohomology classes indexed by an infinite set of square-free integral ideals of the base field 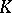 . These elements satisfy certain compatibility conditions. Generally, almost all known Euler systems satisfy the condition ES) described below. Let
. These elements satisfy certain compatibility conditions. Generally, almost all known Euler systems satisfy the condition ES) described below. Let 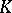 be a number field. Fix a prime number
be a number field. Fix a prime number 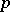 and consider a set
and consider a set 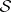 of square-free ideals
of square-free ideals  in
in 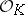 which are relatively prime to some fixed ideal divisible by the primes over
which are relatively prime to some fixed ideal divisible by the primes over 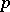 . Let
. Let 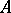 be a finite
be a finite 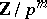 -module with action of
-module with action of 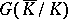 . For each
. For each  , let there be an Abelian extension
, let there be an Abelian extension 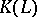 of
of 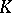 with the property that
with the property that 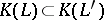 if
if  . Then one wants to construct elements
. Then one wants to construct elements 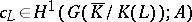 such that:
such that:
ES) 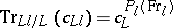 . Here
. Here 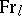 is the Frobenius homomorphism (cf. Frobenius automorphism),
is the Frobenius homomorphism (cf. Frobenius automorphism), 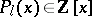 is a polynomial with integral coefficients depending on
is a polynomial with integral coefficients depending on 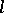 and
and 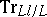 is the transfer mapping from
is the transfer mapping from 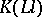 down to
down to 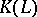 . Next to condition ES), any given Euler system may have additional properties, cf. [a4], [a9], [a10], [a17], [a20], [a22], [a23].
. Next to condition ES), any given Euler system may have additional properties, cf. [a4], [a9], [a10], [a17], [a20], [a22], [a23].
To discover an Euler system is usually a difficult task. Once an Euler system has been identified, one figures out local conditions that the global cohomology classes 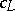 satisfy. Then Kolyvagin's descent procedure gives good control over corresponding arithmetic objects such as the class group of a number field or the Selmer group of an elliptic curve. On the other hand, an Euler system encodes values of the
satisfy. Then Kolyvagin's descent procedure gives good control over corresponding arithmetic objects such as the class group of a number field or the Selmer group of an elliptic curve. On the other hand, an Euler system encodes values of the 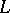 -function connected with the corresponding arithmetic object. In this way Euler systems establish (the sought for) relations between arithmetic objects and corresponding
-function connected with the corresponding arithmetic object. In this way Euler systems establish (the sought for) relations between arithmetic objects and corresponding 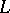 -values.
-values.
Examples.
Some specific Euler systems and objects they compute are listed below.
Cyclotomic units.
This Euler system [a10], [a20] computes eigenspaces (for even characters) of the 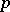 -part of the class group of
-part of the class group of 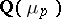 for
for 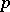 odd. K. Rubin [a20] extended Kolyvagin's method to give an elementary proof of the main conjecture in Iwasawa theory for
odd. K. Rubin [a20] extended Kolyvagin's method to give an elementary proof of the main conjecture in Iwasawa theory for 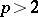 and
and 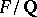 Abelian (with some restrictions on
Abelian (with some restrictions on 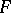 ). In addition, C. Greither [a6] proved the main conjecture (using Kolyvagin's method) for all
). In addition, C. Greither [a6] proved the main conjecture (using Kolyvagin's method) for all 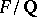 Abelian and all
Abelian and all 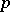 , including
, including 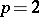 .
.
Twisted Gauss sums.
In this case, the eigenspaces (for odd characters) of the 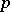 -part of the class group of
-part of the class group of 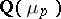 have been computed [a10], [a25].
have been computed [a10], [a25].
Heegner points.
Let 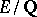 be a modular elliptic curve over
be a modular elliptic curve over 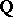 (cf. also Modular curve). In [a9], Kolyvagin used Euler systems of Heegner points to show finiteness of
(cf. also Modular curve). In [a9], Kolyvagin used Euler systems of Heegner points to show finiteness of 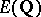 and
and 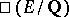 under the assumption that
under the assumption that 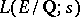 is non-zero at
is non-zero at 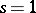 (cf. also Dirichlet
(cf. also Dirichlet 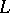 -function). This result was further generalized to certain higher-dimensional modular Abelian varieties (see [a12] and [a13]).
-function). This result was further generalized to certain higher-dimensional modular Abelian varieties (see [a12] and [a13]).
Let 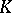 be an imaginary quadratic field of discriminant relatively prime to the conductor of
be an imaginary quadratic field of discriminant relatively prime to the conductor of 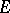 . Kolyvagin applied the Euler system of Heegner points [a10] in case the Heegner point
. Kolyvagin applied the Euler system of Heegner points [a10] in case the Heegner point 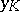 in
in 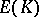 is of infinite order (see also [a7] and [a15] for descriptions of this work). He proved that the following statements hold:
is of infinite order (see also [a7] and [a15] for descriptions of this work). He proved that the following statements hold:
a) 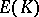 has rank one;
has rank one;
b) 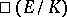 is finite;
is finite;
c) under certain assumptions on 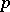 (see [a15], pp. 295–296) the following inequality holds:
(see [a15], pp. 295–296) the following inequality holds:
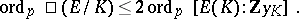 |
Subsequently, in [a11] Kolyvagin proved that the inequality above is actually an equality and determined the structure of 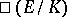 . This Euler system is constructed in cohomology with coefficients in the module
. This Euler system is constructed in cohomology with coefficients in the module 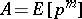 , the
, the 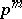 torsion points on the elliptic curve
torsion points on the elliptic curve 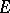 .
.
M. Bertolini and H. Darmon also constructed cohomology classes based on Heegner points [a2]. Using these classes they proved finiteness of certain twisted Mordell–Weil groups for an Abelian variety 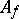 (see [a2]) under the assumption that the corresponding twist of the
(see [a2]) under the assumption that the corresponding twist of the  function of
function of 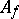 is non-zero at
is non-zero at 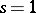 .
.
Elliptic units.
K. Rubin considered an elliptic curve 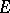 over
over 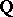 which has complex multiplication (cf. Elliptic curve) by
which has complex multiplication (cf. Elliptic curve) by 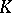 . He applied the Euler system of elliptic units to prove one- and two-variable main conjectures in Iwasawa theory. Using this he obtained (under the assumption that
. He applied the Euler system of elliptic units to prove one- and two-variable main conjectures in Iwasawa theory. Using this he obtained (under the assumption that 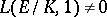 ):
):
A) finiteness of 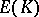 ;
;
B) finiteness of 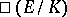 ;
;
C) a Birch–Swinnerton-Dyer formula for 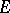 up to some very small explicit factors. Rubin proved that the Birch–Swinnerton-Dyer conjecture holds unconditionally for curves
up to some very small explicit factors. Rubin proved that the Birch–Swinnerton-Dyer conjecture holds unconditionally for curves 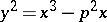 for
for 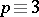 modulo
modulo 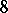 .
.
In the above examples (of cyclotomic units, twisted Gauss sums and elliptic units), the module of coefficients equals 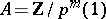 . A number of problems in arithmetic involve the construction of Euler systems with
. A number of problems in arithmetic involve the construction of Euler systems with 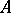 different from
different from  , as is the case for Heegner points.
, as is the case for Heegner points.
Soulé's cyclotomic elements.
M. Kurihara [a14] found an Euler system 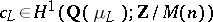 based on a construction done by C. Soulé [a26]. The elements
based on a construction done by C. Soulé [a26]. The elements 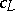 are made of cyclotomic units twisted by the Tate module and sent down to an appropriate field level by the co-restriction mapping. Kurihara used this Euler system to estimate
are made of cyclotomic units twisted by the Tate module and sent down to an appropriate field level by the co-restriction mapping. Kurihara used this Euler system to estimate 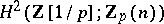 in terms of the index of the Soulé cyclotomic elements inside
in terms of the index of the Soulé cyclotomic elements inside 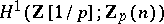 for
for  odd.
odd.
Analogues of Gauss sums for higher 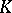 -groups.
-groups.
G. Banaszak and W. Gajda [a1] found an Euler system for higher 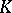 -groups of number fields. It is given in terms of transfer (to an appropriate field level) applied to Gauss sums (as above) multiplied by Bott elements. This system of elements is used to estimate from above the order of the
-groups of number fields. It is given in terms of transfer (to an appropriate field level) applied to Gauss sums (as above) multiplied by Bott elements. This system of elements is used to estimate from above the order of the 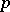 part of the group of divisible elements in
part of the group of divisible elements in 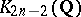 for
for  even. One can map this Euler system via the Dwyer–Fiedlander homomorphism and obtain an Euler system in cohomology. Actually, one obtains elements
even. One can map this Euler system via the Dwyer–Fiedlander homomorphism and obtain an Euler system in cohomology. Actually, one obtains elements 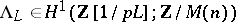 which form an Euler system.
which form an Euler system.
Heegner cycles.
J. Nekovaŕ [a18] discovered an Euler system for a submodule  of the
of the 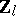 -module
-module 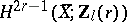 , where
, where 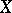 is a Kuga–Sato variety attached to a modular form of weight
is a Kuga–Sato variety attached to a modular form of weight 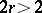 . He used Heegner cycles in
. He used Heegner cycles in 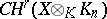 . The elements thus constructed live in
. The elements thus constructed live in 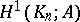 , where
, where 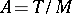 . Similarly to Kolyvagin, he could prove that the Tate–Shafarevich group for the module
. Similarly to Kolyvagin, he could prove that the Tate–Shafarevich group for the module  is finite and that its order divides the square of the index
is finite and that its order divides the square of the index
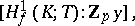 |
which is also proven to be finite. Recently (1997), A. Besser [a3] refined the results of Nekovaŕ. He defined the Tate–Shafarevich group considering also the "bad primes" . For each 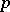 away from the "bad primes" , he found annihilators (determined by the Heegner cycles) of the
away from the "bad primes" , he found annihilators (determined by the Heegner cycles) of the 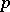 part of the Tate–Shafarevich group.
part of the Tate–Shafarevich group.
Euler systems for 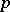 -adic representations.
-adic representations.
Assuming the existence of an Euler system for a 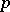 -adic representation
-adic representation 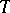 of
of 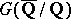 , K. Kato [a8], B. Perin-Riou [a19] and K. Rubin [a24] derived bounds for the Selmer group of the dual representation
, K. Kato [a8], B. Perin-Riou [a19] and K. Rubin [a24] derived bounds for the Selmer group of the dual representation 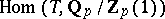 . K. Kato constructed such an Euler system, the Kato Euler system, in the case when
. K. Kato constructed such an Euler system, the Kato Euler system, in the case when 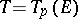 , the Tate module of a modular elliptic curve without complex multiplication (cf. [a24], [a27]). Let
, the Tate module of a modular elliptic curve without complex multiplication (cf. [a24], [a27]). Let 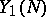 be a quotient of an open modular curve
be a quotient of an open modular curve 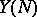 (see [a27]). To start with, Kato constructed an element in
(see [a27]). To start with, Kato constructed an element in 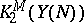 which is a symbol of two carefully chosen modular units. Then, by a series of natural mappings and a clever twisting trick, he mapped these elements to the group
which is a symbol of two carefully chosen modular units. Then, by a series of natural mappings and a clever twisting trick, he mapped these elements to the group
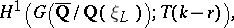 |
where 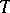 is a
is a 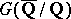 equivariant
equivariant 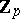 -lattice in a
-lattice in a 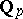 -vector space
-vector space 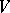 and
and 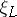 is the
is the 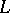 th power root of unity. The vector space
th power root of unity. The vector space  is a quotient of
is a quotient of
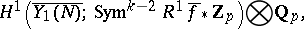 |
where 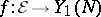 is the natural mapping from the universal elliptic curve down to
is the natural mapping from the universal elliptic curve down to 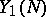 and
and 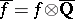 . Under the assumption that
. Under the assumption that 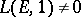 , Kato proved the finiteness of the Tate–Shafarevich and Mordel–Weil groups. In this way, he also reproved Kolyvagin's result on Heegner points (see above). Nevertheless, the work of Kato avoided reference to many analytic results (see [a24], Chap. 7; 8).
, Kato proved the finiteness of the Tate–Shafarevich and Mordel–Weil groups. In this way, he also reproved Kolyvagin's result on Heegner points (see above). Nevertheless, the work of Kato avoided reference to many analytic results (see [a24], Chap. 7; 8).
Work of M. Flach.
Interesting and useful cohomology classes were constructed by M. Flach [a5]. These elements were independently found by S. Bloch and were used by S.J.M. Mildenhall in [a16]. Flach considered a modular elliptic curve 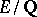 with a modular parametrization
with a modular parametrization 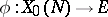 . Let
. Let 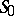 be the set of prime numbers containing
be the set of prime numbers containing 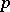 and the primes where
and the primes where 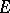 has bad reduction. For each prime number
has bad reduction. For each prime number 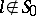 , Flach constructed an element
, Flach constructed an element  which is the image (via a series of natural mappings) of an element in
which is the image (via a series of natural mappings) of an element in 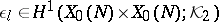 . The elements
. The elements 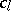 seem to be a first step of some (still unknown, 1998) Euler system. Nevertheless, Flach was able to prove the finiteness of the Selmer and Tate–Shafarevich groups associated with the module
seem to be a first step of some (still unknown, 1998) Euler system. Nevertheless, Flach was able to prove the finiteness of the Selmer and Tate–Shafarevich groups associated with the module 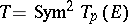 . Actually, he proved that these groups are annihilated by
. Actually, he proved that these groups are annihilated by 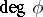 .
.
Constructing interesting elements in cohomology, especially Euler system elements, is a major task of contemporary arithmetic. The interplay between arithmetic and algebraic geometry, analysis (both 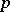 -adic and complex), number theory, etc. has brought about many interesting examples.
-adic and complex), number theory, etc. has brought about many interesting examples.
References
| [a1] | G. Banaszak, W. Gajda, "Euler systems for higher K-theory of number fields" J. Number Th. , 58 : 2 (1996) pp. 213–252 |
| [a2] | M. Bertolini, H. Darmon, "A rigid analytic Gross–Zagier formula and arithmetic applications" preprint |
| [a3] | A. Besser, "On the finiteness of  for motives associated to modular forms" Doc. Math. J. Deutsch. Math. Ver. , 2 (1997) pp. 31–46 for motives associated to modular forms" Doc. Math. J. Deutsch. Math. Ver. , 2 (1997) pp. 31–46 |
| [a4] | H. Darmon, "Euler systems and refined conjectures of Birch Swinnerton–Dyer type" Contemp. Math. , 165 (1994) pp. 265–276 |
| [a5] | M. Flach, "A finiteness theorem for the symmetric square of an elliptic curve" Invent. Math. , 109 (1992) pp. 307–327 |
| [a6] | C. Greither, "Class groups of abelian fields and the main conjecture" Ann. Inst. Fourier (Grenoble) , 42 No 3 (1992) pp. 449–499 |
| [a7] | B.H. Gross, "Kolyvagin's work on modular elliptic curves" J. Coates (ed.) M.J. Taylor (ed.) ,  -Functions and Arithmetic. Proc. Symp. Durham 1989 , London Math. Soc. Lecture Notes , 153 (1991) pp. 235–256 -Functions and Arithmetic. Proc. Symp. Durham 1989 , London Math. Soc. Lecture Notes , 153 (1991) pp. 235–256 |
| [a8] | K. Kato, "Euler systems, Iwasawa theory and Selmer groups" to appear |
| [a9] | V.A. Kolyvagin, "Finitness of 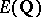 and and 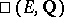 for a class of Weil curves" Izv. Akad. Nauk SSSR , 52 (1988) pp. 522–540 for a class of Weil curves" Izv. Akad. Nauk SSSR , 52 (1988) pp. 522–540 |
| [a10] | V.A. Kolyvagin, "Euler Systems" , Grothendieck Festschrift II , Progr. Math. , 87 , Birkhäuser (1990) pp. 435–483 |
| [a11] | V.A. Kolyvagin, "On the structure of Shafarevich–Tate groups" S. Bloch (ed.) I. Dolgachev (ed.) W. Fulton (ed.) , Algebraic Geometry , Lecture Notes Math. , 1479 (1991) pp. 333–400 |
| [a12] | V.A. Kolyvagin, D.Y. Logacev, "Finiteness of Shafarevich–Tate group and the group of rational points for some modular Abelian varieties" Algebra i Anal. , 1 (1989) pp. 171–196 |
| [a13] | V.A. Kolyvagin, D.Y. Logacev, "Finiteness of  over totally real fields" Izv. Akad. Nauk SSSR Ser. Math. , 55 (1991) pp. 851–876 over totally real fields" Izv. Akad. Nauk SSSR Ser. Math. , 55 (1991) pp. 851–876 |
| [a14] | M. Kurihara, "Some remarks on conjectures about cyclotomic fields and K-groups of 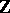 " Compositio Math. , 81 (1992) pp. 223–236 " Compositio Math. , 81 (1992) pp. 223–236 |
| [a15] | W.G. Mccallum, "Kolyvagin's work on Shafarevich–Tate groups" J. Coates (ed.) M.J. Taylor (ed.) ,  -Functions and Arithmetic. Proc. Symp. Durham 1989 , London Math. Soc. Lecture Notes , 153 (1991) pp. 295–316 -Functions and Arithmetic. Proc. Symp. Durham 1989 , London Math. Soc. Lecture Notes , 153 (1991) pp. 295–316 |
| [a16] | S.J.M. Mildenhall, "Cycles in products of elliptic curves and a group analogous to the class group" Duke Math. J. , 67, No.2 (1992) pp. 387–406 |
| [a17] | J. Nekovaŕ, "Values of  -functions and -functions and 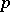 -adic cohomology" preprint (1992) -adic cohomology" preprint (1992) |
| [a18] | J. Nekovaŕ, "Kolyvagin's method for Chow groups of Kuga–Sato varieties" Invent. Math. , 107 (1992) pp. 99–125 |
| [a19] | B. Perrin-Riou, "Systèmes d'Euler 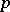 -adiques et théorie d'Iwasawa" Ann. Inst. Fourier , 48 : 5 (1998) pp. 1231–1307 -adiques et théorie d'Iwasawa" Ann. Inst. Fourier , 48 : 5 (1998) pp. 1231–1307 |
| [a20] | K. Rubin, "A proof of some `main conjectures' via methods of Kolyvagin" preprint (1988) |
| [a21] | K. Rubin, "On the main conjecture of Iwasawa theory for imaginary quadratic fields" Invent. Math. , 93 (1988) pp. 701–713 |
| [a22] | K. Rubin, "The `main conjectures' of Iwasawa theory for imaginary quadratic fields" Invent. Math. , 103 (1991) pp. 25–68 |
| [a23] | K. Rubin, "Stark units and Kolyvagin's `Euler systems'" J. Reine Angew. Math. , 425 (1992) pp. 141–154 |
| [a24] | K. Rubin, "Euler systems and modular elliptic curves" preprint (1997) |
| [a25] | K. Rubin, "Kolyvagin's systems of Gauss sums" G. van der Geer (ed.) F. Oort (ed.) J. Steenbrink (ed.) , Arithmetic Algebraic Geometry , Progr. Math. , Birkhäuser (1991) pp. 309–324 |
| [a26] | C. Soulé, "On higher 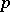 -adic regulators" , Algebraic K-theory, Evanston, 1980 , Lecture Notes Math. , 854 , Springer (1981) pp. 372–401 -adic regulators" , Algebraic K-theory, Evanston, 1980 , Lecture Notes Math. , 854 , Springer (1981) pp. 372–401 |
| [a27] | A. Scholl, "Symbols and Euler systems for modular varieties" preprint |
| [a28] | F. Thaine, "On the ideal class groups of real abelian number fields" Ann. of Math. , 128 (1988) pp. 1–18 |
Euler systems for number fields. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_systems_for_number_fields&oldid=12377