Killing form
A certain bilinear form on a finite-dimensional Lie algebra, introduced by W. Killing . Let 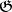 be a finite-dimensional Lie algebra over a field
be a finite-dimensional Lie algebra over a field 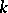 . By the Killing form on
. By the Killing form on 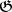 is meant the bilinear form
is meant the bilinear form
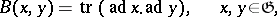 |
where 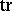 denotes the trace of a linear operator, and
denotes the trace of a linear operator, and 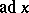 is the image of
is the image of  under the adjoint representation of
under the adjoint representation of 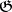 (cf. also Adjoint representation of a Lie group), i.e. the linear operator on the vector space
(cf. also Adjoint representation of a Lie group), i.e. the linear operator on the vector space 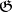 defined by the rule
defined by the rule 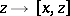 , where
, where 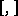 is the commutation operator in the Lie algebra
is the commutation operator in the Lie algebra 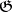 . The Killing form is symmetric. The operators
. The Killing form is symmetric. The operators 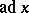 ,
, 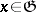 , are skew-symmetric with respect to the Killing form, that is,
, are skew-symmetric with respect to the Killing form, that is,
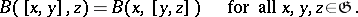 |
If 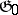 is an ideal of
is an ideal of 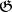 , then the restriction of the Killing form to
, then the restriction of the Killing form to 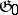 is the same as the Killing form of
is the same as the Killing form of 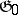 . Each commutative ideal
. Each commutative ideal 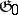 is contained in the kernel of the Killing form. If the Killing form is non-degenerate, then the algebra
is contained in the kernel of the Killing form. If the Killing form is non-degenerate, then the algebra 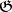 is semi-simple (cf. Lie algebra, semi-simple).
is semi-simple (cf. Lie algebra, semi-simple).
Suppose that the characteristic of the field 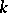 is 0. Then the radical of
is 0. Then the radical of 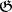 is the same as the orthocomplement with respect to the Killing form of the derived subalgebra
is the same as the orthocomplement with respect to the Killing form of the derived subalgebra 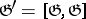 . The algebra
. The algebra 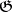 is solvable (cf. Lie algebra, solvable) if and only if
is solvable (cf. Lie algebra, solvable) if and only if 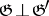 , i.e. when
, i.e. when 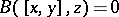 for all
for all 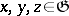 (Cartan's solvability criterion). If
(Cartan's solvability criterion). If 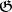 is nilpotent (cf. Lie algebra, nilpotent), then
is nilpotent (cf. Lie algebra, nilpotent), then 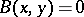 for all
for all 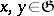 . The algebra
. The algebra 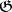 is semi-simple if and only if the Killing form is non-degenerate (Cartan's semi-simplicity criterion).
is semi-simple if and only if the Killing form is non-degenerate (Cartan's semi-simplicity criterion).
Every complex semi-simple Lie algebra contains a real form 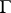 (the compact Weyl form, see Complexification of a Lie algebra) on which the Killing form is negative definite.
(the compact Weyl form, see Complexification of a Lie algebra) on which the Killing form is negative definite.
References
| [1a] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen I" Math. Ann. , 31 (1888) pp. 252–290 |
| [1b] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen II" Math. Ann. , 33 (1889) pp. 1–48 |
| [1c] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen III" Math. Ann. , 34 (1889) pp. 57–122 |
| [1d] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen IV" Math. Ann. , 36 (1890) pp. 161–189 |
| [2] | E. Cartan, "Sur la structure des groupes de transformations finis et continus" , Oevres Complètes , 1 , CNRS (1984) pp. 137–288 |
| [3] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [4] | I. Kaplansky, "Lie algebras and locally compact groups" , Chicago Univ. Press (1971) |
| [5] | M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) |
Comments
The Killing form is a key tool in the Killing–Cartan classification of semi-simple Lie algebras over fields 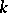 of characteristic 0. If
of characteristic 0. If 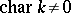 , the Killing form on a semi-simple Lie algebra may be degenerate.
, the Killing form on a semi-simple Lie algebra may be degenerate.
The Killing form is also called the Cartan–Killing form.
Let 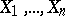 be a basis for the Lie algebra
be a basis for the Lie algebra 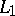 , and let the corresponding structure constants be
, and let the corresponding structure constants be 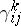 , so that
, so that 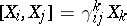 (summation convention). Then in terms of these structure constants the Killing form is given by
(summation convention). Then in terms of these structure constants the Killing form is given by
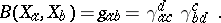 |
The metric (tensor) 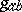 is called the Cartan metric, especially in the theoretical physics literature. Using
is called the Cartan metric, especially in the theoretical physics literature. Using 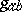 one can lower indices (cf. Tensor on a vector space) to obtain "structure constants"
one can lower indices (cf. Tensor on a vector space) to obtain "structure constants" 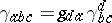 which are completely anti-symmetric in their indices. (A direct consequence of the Jacobi identity and equivalent to the anti-symmetry of the operator
which are completely anti-symmetric in their indices. (A direct consequence of the Jacobi identity and equivalent to the anti-symmetry of the operator 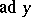 with respect to
with respect to 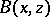 ; cf. above.)
; cf. above.)
References
| [a1] | L. O'Raifeartaigh, "Group structure of gauge theories" , Cambridge Univ. Press (1986) |
| [a2] | V.S. Varadarajan, "Lie groups, Lie algebras and their representations" , Springer, reprint (1984) |
| [a3] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 |
Killing form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Killing_form&oldid=12372