Operator topology
A topology on the space 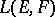 of continuous linear mappings from one topological vector space
of continuous linear mappings from one topological vector space 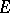 into another topological vector space
into another topological vector space 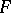 , converting the space
, converting the space 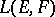 into a topological vector space. Let
into a topological vector space. Let 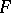 be a locally convex space and let
be a locally convex space and let 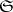 be a family of bounded subsets of
be a family of bounded subsets of 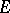 such that the linear hull of the union of the sets of this family is dense in
such that the linear hull of the union of the sets of this family is dense in 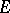 . Let
. Let 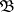 be a basis of neighbourhoods of zero in
be a basis of neighbourhoods of zero in 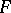 . The family
. The family
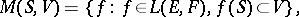 |
where 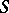 runs through
runs through 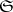 and
and 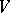 through
through 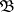 , is a basis of neighbourhoods of zero for a unique topology that is invariant with respect to translation, which is an operator topology and which converts the space
, is a basis of neighbourhoods of zero for a unique topology that is invariant with respect to translation, which is an operator topology and which converts the space 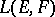 into a locally convex space; this topology is called the
into a locally convex space; this topology is called the 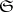 -topology on
-topology on 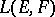 .
.
Examples. I) Let 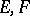 be locally convex spaces. 1) Let
be locally convex spaces. 1) Let 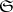 be the family of all finite subsets in
be the family of all finite subsets in 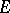 ; the corresponding
; the corresponding 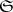 -topology (on
-topology (on 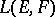 ) is called the topology of simple (or pointwise) convergence. 2) Let
) is called the topology of simple (or pointwise) convergence. 2) Let 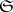 be the family of all convex balanced compact subsets of
be the family of all convex balanced compact subsets of 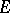 ; the corresponding topology is called the topology of convex balanced compact convergence. 3) Let
; the corresponding topology is called the topology of convex balanced compact convergence. 3) Let 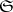 be the family of all pre-compact subsets of
be the family of all pre-compact subsets of 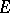 ; the corresponding
; the corresponding 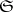 -topology is called the topology of pre-compact convergence. 4) Let
-topology is called the topology of pre-compact convergence. 4) Let 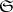 be the family of all bounded subsets; the corresponding topology is called the topology of bounded convergence.
be the family of all bounded subsets; the corresponding topology is called the topology of bounded convergence.
II) If 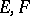 are Banach spaces considered simultaneously in the weak or strong (norm) topology, then the corresponding spaces
are Banach spaces considered simultaneously in the weak or strong (norm) topology, then the corresponding spaces 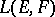 coincide algebraically; the corresponding topologies of simple convergence are called the weak or strong operator topologies on
coincide algebraically; the corresponding topologies of simple convergence are called the weak or strong operator topologies on 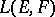 . The strong operator topology majorizes the weak operator topology; both are compatible with the duality between
. The strong operator topology majorizes the weak operator topology; both are compatible with the duality between 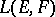 and the space of functionals on
and the space of functionals on 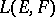 of the form
of the form 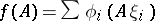 , where
, where 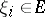 ,
, 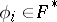 ,
, 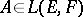 .
.
III) Let 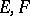 be Hilbert spaces and let
be Hilbert spaces and let 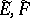 be countable direct sums of the Hilbert spaces
be countable direct sums of the Hilbert spaces 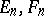 , respectively, where
, respectively, where  ,
, 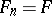 for all integer
for all integer  ; let
; let 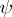 be the imbedding of the space
be the imbedding of the space 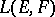 into
into 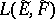 defined by the condition that for any operator
defined by the condition that for any operator 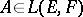 the restriction of the operator
the restriction of the operator 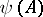 to the subspace
to the subspace 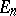 maps
maps 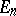 into
into 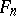 and coincides on
and coincides on 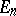 with the operator
with the operator 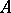 . Then the complete pre-image in
. Then the complete pre-image in 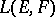 of the weak (strong) operator topology on
of the weak (strong) operator topology on 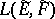 is called the ultra-weak (correspondingly, ultra-strong) operator topology on
is called the ultra-weak (correspondingly, ultra-strong) operator topology on 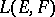 . The ultra-weak (ultra-strong) topology majorizes the weak (strong) operator topology. A symmetric subalgebra
. The ultra-weak (ultra-strong) topology majorizes the weak (strong) operator topology. A symmetric subalgebra 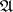 of the algebra
of the algebra 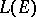 of all bounded linear operators on a Hilbert space
of all bounded linear operators on a Hilbert space 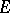 , containing the identity operator, coincides with the set of all operators from
, containing the identity operator, coincides with the set of all operators from 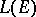 that commute with each operator from
that commute with each operator from 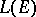 that commutes with all operators from
that commutes with all operators from 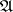 , if and only if
, if and only if 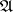 is closed in the weak (or strong, or ultra-weak, or ultra-strong) operator topology, i.e. is a von Neumann algebra.
is closed in the weak (or strong, or ultra-weak, or ultra-strong) operator topology, i.e. is a von Neumann algebra.
References
| [1] | H.H. Schaefer, "Topological vector spaces" , Springer (1971) |
| [2] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Wiley, reprint (1988) |
| [3] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [4] | S. Sakai, "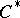 -algebras and -algebras and 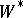 -algebras" , Springer (1971) -algebras" , Springer (1971) |
Operator topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Operator_topology&oldid=12370