Ward theorem

on the differentiation of an additive interval function

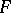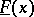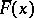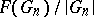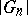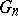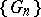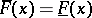Let be a real-valued additive interval function, and let () be the greatest lower (least upper) bound of the limits of the sequences , where is the Lebesgue measure of , and runs through all regular sequences of intervals contracting towards the point . Then the equation is valid almost-everywhere (in the sense of the Lebesgue measure) on the set 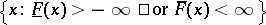. A sequence of intervals 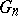is regular if there exist a number 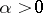and sequences of spheres , 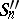such that for all ,

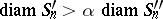and

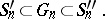If, in the above formulation, the condition of regularity is discarded, Ward's second theorem is obtained. These theorems generalize the Denjoy theorem on derivatives of a function of one variable. The theorems were established by A.J. Ward .

References

[1a]	A.J. Ward, "On the differentiation of additive functions of rectangles" Fund. Math. , 28 (1936) pp. 167–182
[1b]	A.J. Ward, "On the derivation of additive functions of intervals in -dimensional space" Fund. Math. , 28 (1937) pp. 265–279

References

[a1]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)