Reidemeister torsion

de Rham torsion, Franz torsion

An invariant which allows one to distinguish many structures in differential topology, for example knots and smooth structures on manifolds, particularly on lens spaces. Reidemeister torsion was first introduced by K. Reidemeister (see [1]) while studying three-dimensional lenses, the generalization for -dimensional lenses was obtained independently in [2] and [3].

Let be a free complex of left -modules, where is an associative ring with a unit element. Further, let be a matrix representation of , i.e. a homomorphism from into the ring of all real -matrices. Let be distinguished bases in the modules 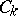of the complex 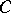, and let the complex of -modules be acyclic; then the Whitehead torsion is defined as , where is the multiplicative group of the field of real numbers. The number is called the Reidemeister torsion of the complex , and also the real Reidemeister torsion.

The usefulness of transforming the Whitehead torsion into the Reidemeister torsion is based on Bass' theorem [4]. If 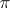is a finite group, then the element has finite order if for any representation , where is the Reidemeister torsion induced by the element .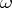

References

[1]	K. Reidemeister, "Homotopieringe und Linsenräume" Abh. Math. Sem. Univ. Hamburg , 11 (1935) pp. 102–109
[2]	W. Franz, "Ueber die Torsion einer Ueberdeckung" J. Reine Angew. Math. , 173 (1935) pp. 245–254
[3]	G. de Rham, "Sur les nouveaux invariants de M. Reidemeister" Mat. Sb. , 1 : 5 (1936) pp. 737–743
[4]	H. Bass, "-theory and stable algebra" Publ. Math. IHES , 22 (1964) pp. 5–60

References

[a1]	J. Milnor, "Whitehead torsion" Bull. Amer. Math. Soc. , 72 (1966) pp. 358–426