Automata, homomorphism of

A mapping of the input and output alphabets and of the set of states of an automaton into analogous sets of a second automaton that preserves the transition and output functions. More precisely, a homomorphism of an automaton into an automaton (cf. Automaton, finite) is a mapping of the set into the set

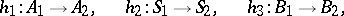such that the following equalities are valid for any from and from :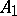

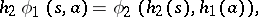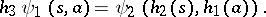Initialized automata are subject to the additional requirement that 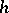maps the initial state to the initial state. The automata 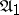and 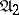are said to be homomorphic if there exists a homomorphism of automata mapping 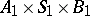into 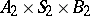. If, in addition, 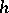is one-to-one, 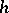is called an isomorphism, and the automata 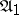and 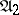are said to be isomorphic automata. If the alphabets and 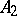, and also the alphabets and 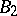, are identical and the mappings 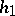and 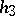are the identity mappings, the homomorphism (isomorphism) 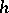is known as a state homomorphism (state isomorphism). Input and output homomorphisms (isomorphisms) are defined in a similar manner. State-isomorphic automata and state-homomorphic initialized automata are equivalent (cf. Automata, equivalence of).

The concept of a homomorphism of automata is used in the context of problems concerning minimization, decomposition and completeness of automata, among others.

References

[1]	V.M. Glushkov, "The abstract theory of automata" Russian Math. Surveys , 16 : 5 (1961) pp. 1–53 Uspekhi Mat. Nauk , 16 : 5 (1961) pp. 3–62