Function vanishing at infinity
From Encyclopedia of Mathematics
Let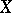 
be a topological space. A real- or complex-valued function on 
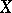is said to vanish at infinity if for each 
there is a compact set 
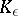such that 
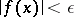for all 
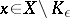. For non-compact 
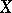, such a function can be extended to a continuous function on the one-point compactification 
of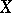 
(with value 
at 
).
The algebra of functions on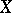 
vanishing at infinity is denoted by 
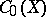. In many cases 
determines 
, see e.g. Banach–Stone theorem. If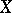 
is compact, 
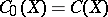. The space 
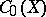identifies with 
.
References
| [a1] | E. Behrends, "M-structure and the Banach–Stone theorem" , Springer (1979) |
| [a2] | K. Jarosz, "Perturbations of Banach spaces" , Springer (1985) |
How to Cite This Entry:
Function vanishing at infinity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Function_vanishing_at_infinity&oldid=12325
Function vanishing at infinity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Function_vanishing_at_infinity&oldid=12325
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article