Covering homotopy
for a homotopy  of a mapping
of a mapping  , given a mapping
, given a mapping 
A homotopy  such that
such that  . In this situation, if the covering mapping
. In this situation, if the covering mapping  for
for  is prescribed in advance, one says that
is prescribed in advance, one says that  extends
extends  . The covering homotopy axiom, in its strong version, requires that, for a given mapping
. The covering homotopy axiom, in its strong version, requires that, for a given mapping  , for any homotopy
, for any homotopy  from a paracompactum
from a paracompactum  and for any
and for any  (
( ), an extension of
), an extension of  to a covering homotopy
to a covering homotopy  exists. In that case
exists. In that case  is said to be a Hurewicz fibration. The most important example is provided by the locally trivial fibre bundles (cf. Locally trivial fibre bundle). If the covering homotopy property is only required to hold in the case that
is said to be a Hurewicz fibration. The most important example is provided by the locally trivial fibre bundles (cf. Locally trivial fibre bundle). If the covering homotopy property is only required to hold in the case that  is a finite polyhedron,
is a finite polyhedron, 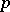 is called a Serre fibration.
is called a Serre fibration.
Let  and
and 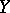 be arcwise connected and let
be arcwise connected and let 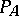 be the path space of
be the path space of  (i.e. the space of continuous mappings
(i.e. the space of continuous mappings  ). Consider a continuous mapping
). Consider a continuous mapping
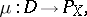 |
where
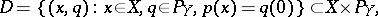 |
and assume that  begins at a point
begins at a point  and covers
and covers  . Then the formula
. Then the formula 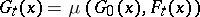 yields an extension of
yields an extension of  to a covering homotopy
to a covering homotopy  . In particular, a mapping
. In particular, a mapping  satisfying these conditions can be defined naturally for a covering, and also for a smooth vector bundle with a fixed connection. The validity of the covering homotopy axiom in Serre's formulation makes it possible to construct the exact homotopy sequence of a fibration (see Homotopy group).
satisfying these conditions can be defined naturally for a covering, and also for a smooth vector bundle with a fixed connection. The validity of the covering homotopy axiom in Serre's formulation makes it possible to construct the exact homotopy sequence of a fibration (see Homotopy group).
Comments
Thus, a covering homotopy is a lifting of a given homotopy (a homotopy lifting). The covering homotopy property is dual to the homotopy extension property, which defines the notion of a cofibration.
References
| [a1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. Chapt. 2 |
Covering homotopy. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Covering_homotopy&oldid=12314