A continuous Markov process 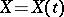 with transition density
with transition density 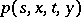 which satisfies the following condition: There exist functions
which satisfies the following condition: There exist functions 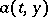 and
and 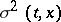 , known as the drift coefficient and the diffusion coefficient respectively, such that for any
, known as the drift coefficient and the diffusion coefficient respectively, such that for any 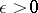 ,
,
 | (1) |
it being usually assumed that these limit relations are uniform with respect to 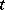 in each finite interval
in each finite interval 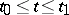 and with respect to
and with respect to  ,
, 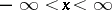 . An important representative of this class of processes is the process of Brownian motion, which was originally considered as a mathematical model of diffusion processes (hence the name "diffusion process" ).
. An important representative of this class of processes is the process of Brownian motion, which was originally considered as a mathematical model of diffusion processes (hence the name "diffusion process" ).
If the transition density 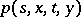 is continuous in
is continuous in  and
and  together with its derivatives
together with its derivatives  and
and 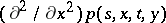 , it is the fundamental solution of the differential equation
, it is the fundamental solution of the differential equation
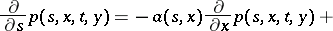 | (2) |
which is known as the backward Kolmogorov equation (cf. also Kolmogorov equation).
In the homogeneous case, when the drift coefficient 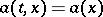 and the diffusion coefficient
and the diffusion coefficient 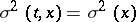 are independent of the time
are independent of the time 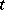 , the backward Kolmogorov equation for the respective transition density
, the backward Kolmogorov equation for the respective transition density 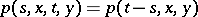 has the form
has the form
If the transition density 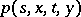 has a continuous derivative
has a continuous derivative  in
in 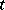 and
and 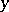 such that the functions
such that the functions 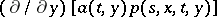 and
and 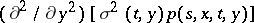 are continuous in
are continuous in 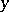 , it is the fundamental solution of the differential equation
, it is the fundamental solution of the differential equation
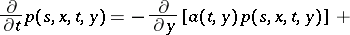 | (3) |
known as the Fokker–Planck equation, or the forward Kolmogorov equation. The differential equations (2) and (3) for the probability density are the fundamental analytic objects of study of diffusion processes. There is also another, purely "probabilistic" , approach to diffusion processes, based on the representation of the process 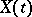 as the solution of the Itô stochastic differential equation
as the solution of the Itô stochastic differential equation
where 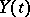 is the standard process of Brownian motion. Roughly speaking,
is the standard process of Brownian motion. Roughly speaking, 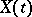 is considered to be connected with some Brownian motion process
is considered to be connected with some Brownian motion process 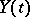 in such a way that if
in such a way that if 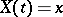 , then the increment
, then the increment 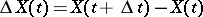 during the next period of time
during the next period of time 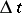 is
is
If this asymptotic relation is understood in the sense that
where  are magnitudes of the same type as in equations (1), the
are magnitudes of the same type as in equations (1), the 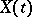 under consideration will constitute a diffusion process in the sense of this definition as well.
under consideration will constitute a diffusion process in the sense of this definition as well.
Multi-dimensional diffusion process is the name usually given to a continuous Markov process 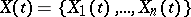 in an
in an  -dimensional vector space
-dimensional vector space 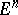 whose transition density
whose transition density 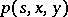 satisfies the following conditions: For any
satisfies the following conditions: For any 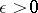 ,
,
The vector  characterizes the local drift of the process
characterizes the local drift of the process 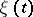 , and the matrix
, and the matrix 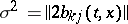 ,
, 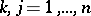 , characterizes the mean square deviation of the random process
, characterizes the mean square deviation of the random process 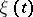 from the initial position
from the initial position  in a small period of time between
in a small period of time between 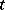 and
and 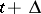 .
.
Subject to certain additional restrictions, the transition density 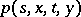 of a multi-dimensional diffusion process satisfies the forward and backward Kolmogorov differential equations:
of a multi-dimensional diffusion process satisfies the forward and backward Kolmogorov differential equations:
A multi-dimensional diffusion process 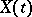 may also be described with the aid of Itô's stochastic differential equations:
may also be described with the aid of Itô's stochastic differential equations:
where 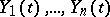 are mutually-independent Brownian motion processes, while
are mutually-independent Brownian motion processes, while
are the eigen vectors of the matrix 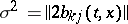 .
.
References
| [1] | I.I. Gikhman, A.V. Skorokhod, "Introduction to the theory of random processes" , Saunders (1969) (Translated from Russian) |
| [2] | I.I. Gikhman, A.V. Skorokhod, "Stochastic differential equations and their applications" , Springer (1972) (Translated from Russian) |
Instead of backward Kolmogorov equation and forward Kolmogorov equation are also finds simply backward equation and forward equation.
References
| [a1] | N. Ikeda, S. Watanabe, "Stochastic differential equations and diffusion processes" , North-Holland & Kodansha (1981) |
| [a2] | D.W. Stroock, S.R.S. Varadhan, "Multidimensional diffusion processes" , Springer (1979) |
| [a3] | L. Arnold, "Stochastische Differentialgleichungen" , R. Oldenbourg (1973) (Translated from Russian) |
How to Cite This Entry:
Diffusion process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diffusion_process&oldid=12304
This article was adapted from an original article by Yu.A. Rozanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article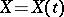 with transition density
with transition density 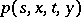 which satisfies the following condition: There exist functions
which satisfies the following condition: There exist functions 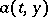 and
and 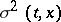 , known as the drift coefficient and the diffusion coefficient respectively, such that for any
, known as the drift coefficient and the diffusion coefficient respectively, such that for any 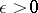 ,
,

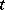 in each finite interval
in each finite interval 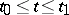 and with respect to
and with respect to  ,
, 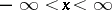 . An important representative of this class of processes is the process of Brownian motion, which was originally considered as a mathematical model of diffusion processes (hence the name "diffusion process" ).
. An important representative of this class of processes is the process of Brownian motion, which was originally considered as a mathematical model of diffusion processes (hence the name "diffusion process" ).
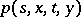 is continuous in
is continuous in  and
and  together with its derivatives
together with its derivatives  and
and 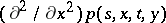 , it is the fundamental solution of the differential equation
, it is the fundamental solution of the differential equation
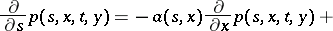
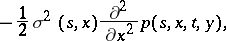
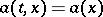 and the diffusion coefficient
and the diffusion coefficient 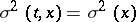 are independent of the time
are independent of the time 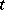 , the backward Kolmogorov equation for the respective transition density
, the backward Kolmogorov equation for the respective transition density 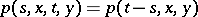 has the form
has the form
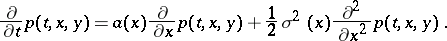
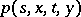 has a continuous derivative
has a continuous derivative  in
in 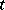 and
and 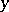 such that the functions
such that the functions 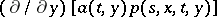 and
and 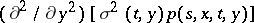 are continuous in
are continuous in 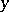 , it is the fundamental solution of the differential equation
, it is the fundamental solution of the differential equation
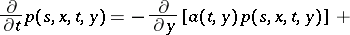
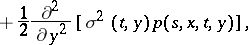
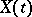 as the solution of the Itô stochastic differential equation
as the solution of the Itô stochastic differential equation
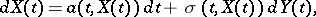
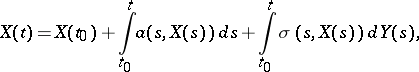
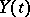 is the standard process of Brownian motion. Roughly speaking,
is the standard process of Brownian motion. Roughly speaking, 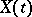 is considered to be connected with some Brownian motion process
is considered to be connected with some Brownian motion process 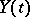 in such a way that if
in such a way that if 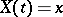 , then the increment
, then the increment 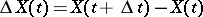 during the next period of time
during the next period of time 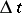 is
is
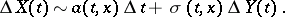
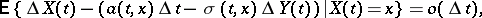
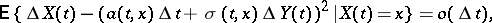
 are magnitudes of the same type as in equations (1), the
are magnitudes of the same type as in equations (1), the 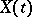 under consideration will constitute a diffusion process in the sense of this definition as well.
under consideration will constitute a diffusion process in the sense of this definition as well.
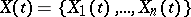 in an
in an  -dimensional vector space
-dimensional vector space 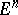 whose transition density
whose transition density 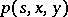 satisfies the following conditions: For any
satisfies the following conditions: For any 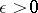 ,
,
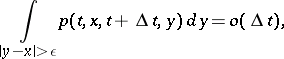
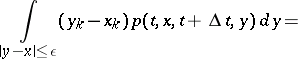
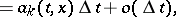
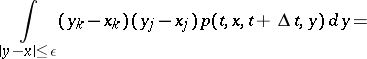
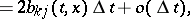
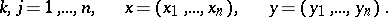
 characterizes the local drift of the process
characterizes the local drift of the process 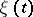 , and the matrix
, and the matrix 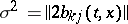 ,
, 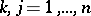 , characterizes the mean square deviation of the random process
, characterizes the mean square deviation of the random process 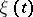 from the initial position
from the initial position  in a small period of time between
in a small period of time between 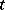 and
and 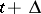 .
.
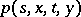 of a multi-dimensional diffusion process satisfies the forward and backward Kolmogorov differential equations:
of a multi-dimensional diffusion process satisfies the forward and backward Kolmogorov differential equations:
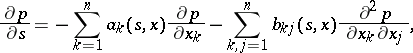
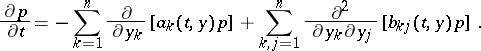
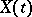 may also be described with the aid of Itô's stochastic differential equations:
may also be described with the aid of Itô's stochastic differential equations:
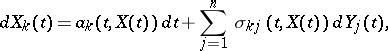
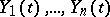 are mutually-independent Brownian motion processes, while
are mutually-independent Brownian motion processes, while
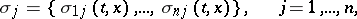
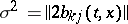 .
.