Semi-simple matrix

A square matrix over a field 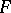similar to a matrix of the form , where is a matrix over whose characteristic polynomial is irreducible in 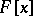, 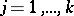(cf. Irreducible polynomial). For a matrix over a field , the following three statements are equivalent: 1) is semi-simple; 2) the minimum polynomial of 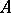has no multiple factors in 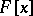; and 3) the algebra 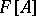is semi-simple (cf. Semi-simple algebra).

If 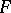is a perfect field, then a semi-simple matrix over 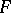is similar to a diagonal matrix over a certain extension of 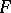. For any square matrix 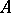over a perfect field there is a unique representation in the form 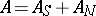, where 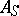is a semi-simple matrix, 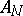is nilpotent and ; the matrices 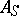and 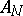belong to the algebra .

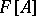References

[1]	N. Bourbaki, "Algèbre" , Eléments de mathématiques , 2 , Hermann (1959)