Fredholm kernel
A Fredholm kernel is a function  defined on
defined on  giving rise to a completely-continuous operator
giving rise to a completely-continuous operator
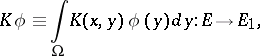 | (*) |
where  is a measurable set in an
is a measurable set in an  -dimensional Euclidean space, and
-dimensional Euclidean space, and  and
and  are function spaces. The operator (*) is called a Fredholm integral operator from
are function spaces. The operator (*) is called a Fredholm integral operator from  into
into  . An important class of Fredholm kernels is that of the measurable functions
. An important class of Fredholm kernels is that of the measurable functions  on
on  for which
for which
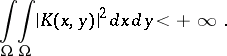 |
A Fredholm kernel that satisfies this condition is also called an  -kernel.
-kernel.
A Fredholm kernel is called degenerate if it can be represented as the sum of a product of functions of  alone by functions of
alone by functions of  alone:
alone:
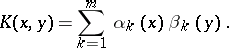 |
If  for almost-all
for almost-all  , then the Fredholm kernel is called symmetric, and if
, then the Fredholm kernel is called symmetric, and if  , it is called Hermitian (here the bar denotes complex conjugation). A Fredholm kernel
, it is called Hermitian (here the bar denotes complex conjugation). A Fredholm kernel  is called skew-Hermitian if
is called skew-Hermitian if 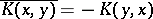 .
.
The Fredholm kernels  and
and 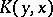 are called transposed or allied, and the kernels
are called transposed or allied, and the kernels 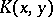 and
and  are called adjoint.
are called adjoint.
References
| [1] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) pp. Chapt. 1 (Translated from Russian) |
Comments
A completely-continuous operator is nowadays usually called a compact operator.
In the main article above, no distinction is made between real-valued and complex-valued kernels. Usually, symmetry is defined for real-valued kernels, as is skew-symmetry:  . Hermiticity and skew-Hermiticity are then properties of complex-valued kernels. However, the terminology in the literature varies wildly.
. Hermiticity and skew-Hermiticity are then properties of complex-valued kernels. However, the terminology in the literature varies wildly.
About the terminology allied (transposed) and adjoint see also (the editorial comments to) Fredholm theorems.
A Fredholm kernel is a bivalent tensor (cf. Tensor on a vector space) giving rise to a Fredholm operator. Let 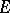 and
and  be locally convex spaces (cf. Locally convex space), and let
be locally convex spaces (cf. Locally convex space), and let  be the completion of the tensor product
be the completion of the tensor product  of these spaces in the inductive topology, that is, in the strongest locally convex topology in which the canonical bilinear mapping
of these spaces in the inductive topology, that is, in the strongest locally convex topology in which the canonical bilinear mapping  is continuous. An element
is continuous. An element  is called a Fredholm kernel if it can be represented in the form
is called a Fredholm kernel if it can be represented in the form
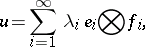 |
where  is a summable sequence of numbers, and
is a summable sequence of numbers, and  and
and  are sequences of elements in some complete convex circled bounded sets in
are sequences of elements in some complete convex circled bounded sets in  and
and  , respectively. Suppose that
, respectively. Suppose that  is the dual (cf. Adjoint space)
is the dual (cf. Adjoint space)  of a locally convex space
of a locally convex space  . Then a Fredholm kernel gives rise to a Fredholm operator
. Then a Fredholm kernel gives rise to a Fredholm operator  of the form
of the form
 |
where  is the value of the functional
is the value of the functional  at the element
at the element  . If
. If  and
and  are Banach spaces, then every element of
are Banach spaces, then every element of  is a Fredholm kernel.
is a Fredholm kernel.
The concept of a Fredholm kernel can also be generalized to the case of the tensor product of several locally convex spaces. Fredholm kernels and Fredholm operators constitute a natural domain of application of the Fredholm theory.
References
| [1] | A. Grothendieck, "La théorie de Fredholm" Bull. Amer. Math. Soc. , 84 (1956) pp. 319–384 |
| [2] | A. Grothendieck, "Produits tensoriels topologiques et espaces nucleaires" Mem. Amer. Math. Soc. , 5 (1955) |
G.L. Litvinov
Comments
A set  in a topological vector space
in a topological vector space  over a normal field
over a normal field  is called circled (or balanced) if
is called circled (or balanced) if  for all
for all  in
in  .
.
Fredholm kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fredholm_kernel&oldid=12278