Morse index
A number associated with a critical point of a smooth function on a manifold or of a geodesic on a Riemannian (or Finsler) manifold.
1) The Morse index of a critical point 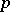 of a smooth function
of a smooth function 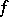 on a manifold
on a manifold 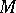 is equal, by definition, to the negative index of inertia of the Hessian of
is equal, by definition, to the negative index of inertia of the Hessian of  at
at 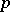 (cf. Hessian of a function), that is, the dimension of the maximal subspace of the tangent space
(cf. Hessian of a function), that is, the dimension of the maximal subspace of the tangent space 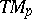 of
of 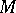 at
at 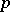 on which the Hessian is negative definite. This definition makes sense also for twice (Fréchet) differentiable functions on infinite-dimensional Banach spaces. The only difference is that the value
on which the Hessian is negative definite. This definition makes sense also for twice (Fréchet) differentiable functions on infinite-dimensional Banach spaces. The only difference is that the value 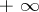 is admissible for the index. In this case it is expedient to introduce the idea of the co-index of a critical point
is admissible for the index. In this case it is expedient to introduce the idea of the co-index of a critical point 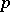 of
of 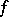 as the positive index of inertia of the Hessian (the second Fréchet differential) of
as the positive index of inertia of the Hessian (the second Fréchet differential) of 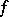 at
at  .
.
2) Let 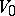 and
and 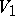 be smooth submanifolds of a complete Riemannian space
be smooth submanifolds of a complete Riemannian space 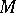 . For a piecewise-smooth path
. For a piecewise-smooth path 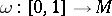 with
with 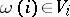 ,
, 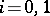 , transversal to
, transversal to 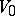 and
and 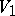 at its end-points
at its end-points 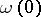 and
and 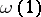 , the analogue of a tangent space is the vector space
, the analogue of a tangent space is the vector space 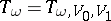 of all piecewise-smooth vector fields
of all piecewise-smooth vector fields 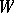 along
along 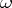 for which
for which 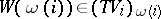 ,
, 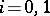 . For any geodesic
. For any geodesic  with
with  , orthogonal at its end-points
, orthogonal at its end-points 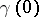 and
and 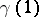 to
to 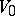 and
and 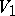 , respectively, the second variation
, respectively, the second variation 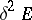 of the action functional (see Morse theory) defines a symmetric bilinear functional
of the action functional (see Morse theory) defines a symmetric bilinear functional 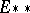 on
on 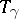 (the analogue of the Hessian). The Morse index of the geodesic is equal, by definition, to the negative index of inertia of this functional. The null space
(the analogue of the Hessian). The Morse index of the geodesic is equal, by definition, to the negative index of inertia of this functional. The null space 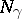 of
of  on
on 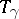 (the set of
(the set of 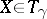 at which
at which 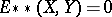 for all
for all 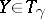 ) consists exactly of the Jacobi fields (cf. Jacobi vector field)
) consists exactly of the Jacobi fields (cf. Jacobi vector field) 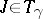 . If
. If 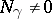 , the geodesic is called
, the geodesic is called 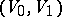 -degenerate, and
-degenerate, and 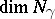 is called the order of degeneracy of the geodesic.
is called the order of degeneracy of the geodesic.
The case when 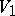 is a point
is a point 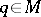 is considered below. Let
is considered below. Let  be the normal bundle to
be the normal bundle to 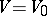 in
in 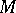 and let
and let 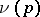 be its fibre over
be its fibre over 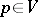 . The restriction of the exponential mapping
. The restriction of the exponential mapping  defines a mapping
defines a mapping 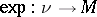 . A geodesic
. A geodesic 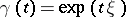 ,
, 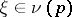 ,
, 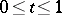 , is
, is 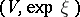 -degenerate if and only if the kernel of the differential
-degenerate if and only if the kernel of the differential 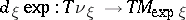 of
of 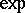 at
at  is not null; in this connection, the dimension of the kernel is equal to the order of degeneracy of the geodesic
is not null; in this connection, the dimension of the kernel is equal to the order of degeneracy of the geodesic 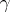 . A point
. A point 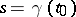 ,
, 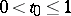 , is called a focal point of
, is called a focal point of 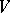 along
along 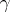 if the geodesic
if the geodesic 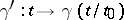 is
is 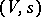 -degenerate; the order of degeneracy of
-degenerate; the order of degeneracy of 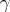 is called the multiplicity of the focal point
is called the multiplicity of the focal point  . By the Sard theorem, the set of focal points has measure zero, so a typical geodesic is non-degenerate. If
. By the Sard theorem, the set of focal points has measure zero, so a typical geodesic is non-degenerate. If  also consists of one point
also consists of one point 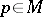 (
( is not excluded), then a focal point is called adjoint to
is not excluded), then a focal point is called adjoint to 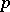 along
along 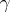 . The Morse index theorem [1] asserts that the Morse index of a geodesic is finite and equal to the number of focal points
. The Morse index theorem [1] asserts that the Morse index of a geodesic is finite and equal to the number of focal points 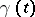 of
of 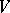 ,
,  , taking account of multiplicity.
, taking account of multiplicity.
References
| [1] | M. Morse, "The calculus of variations in the large" , Amer. Math. Soc. (1934) |
| [2] | W. Ambrose, "The index theorem in Riemannian geometry" Ann. of Math. , 73 (1961) pp. 49–86 |
Comments
There is a natural generalization of the Morse index of geodesics to variational calculus, which runs as follows. Let 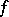 be a real-valued smooth function on an open subset
be a real-valued smooth function on an open subset 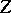 of
of 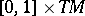 and let
and let 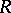 be a smooth submanifold of
be a smooth submanifold of 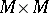 . Let
. Let 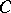 be the space of smooth curves
be the space of smooth curves 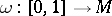 for which the
for which the 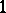 -jet lies in
-jet lies in 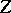 and
and 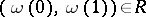 . Then
. Then  is a Banach manifold, on which one has the smooth functional
is a Banach manifold, on which one has the smooth functional
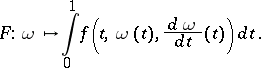 |
One then considers the Morse index of 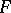 at critical curves
at critical curves 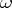 ; it is finite if the Hessian of
; it is finite if the Hessian of 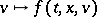 is positive definite at
is positive definite at 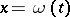 ,
, 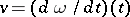 ,
, 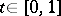 (Legendre's condition, cf. Legendre condition).
(Legendre's condition, cf. Legendre condition).
References
| [a1] | J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963) |
| [a2] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
| [a3] | W. Klingenberg, "Lectures on closed geodesics" , Springer (1978) |
Morse index. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Morse_index&oldid=12274