Cut locus
from a point 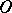
The set of points  of a Riemannian manifold
of a Riemannian manifold 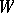 on the geodesic rays emanating from
on the geodesic rays emanating from 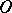 for which the ray
for which the ray 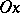 is not extendable as a geodesic beyond the point
is not extendable as a geodesic beyond the point  . In the two-dimensional case the cut locus is a one-dimensional graph with no cycles (see [2]); if
. In the two-dimensional case the cut locus is a one-dimensional graph with no cycles (see [2]); if 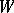 is analytic of arbitrary dimension, then it is a polyhedron of analytic submanifolds (see [3]). The cut locus depends continuously on
is analytic of arbitrary dimension, then it is a polyhedron of analytic submanifolds (see [3]). The cut locus depends continuously on  . The cut locus is defined not only with respect to a point but also with respect to other subsets, for example, the boundary
. The cut locus is defined not only with respect to a point but also with respect to other subsets, for example, the boundary 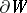 , and also in spaces other than Riemannian manifolds, for example, on convex surfaces (see [4]) and in two-dimensional manifolds of bounded curvature.
, and also in spaces other than Riemannian manifolds, for example, on convex surfaces (see [4]) and in two-dimensional manifolds of bounded curvature.
References
| [1] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [2] | S.B. Myers, "Connections between differential geometry and topology. I Simply connected surfaces" Duke Math. J. , 1 (1935) pp. 376–391 |
| [3] | M.A. Buchner, "Simplicial structure of the real analytic cut locus" Proc. Amer. Math. Soc. , 64 : 1 (1977) pp. 118–121 |
| [4] | J. Kunze, "Der Schnittort auf konvexen Verheftungsflächen" , Springer (1969) |
Comments
"Non-extendable as a geodesic" means that 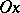 looses the property of minimality after the point
looses the property of minimality after the point  , i.e.
, i.e. 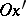 is no longer the minimal path from
is no longer the minimal path from 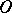 to
to 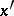 if
if 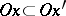 .
.
Cut locus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cut_locus&oldid=12250