Moving-average process
A stochastic process which is stationary in the wide sense and which can be obtained by applying some linear transformation to a process with non-correlated values (that is, to a white noise process). The term is often applied to the more special case of a process 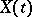 in discrete time
in discrete time 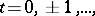 that is representable in the form
that is representable in the form
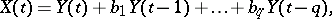 | (1) |
where 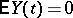 ,
, 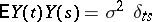 , with
, with 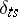 the Kronecker delta (so that
the Kronecker delta (so that 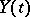 is a white noise process with spectral density
is a white noise process with spectral density 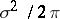 ),
), 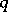 is a positive integer, and
is a positive integer, and 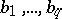 are constant coefficients. The spectral density
are constant coefficients. The spectral density  of such a process is given by
of such a process is given by
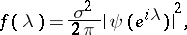 |
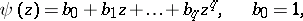 |
and its correlation function 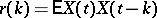 has the form
has the form
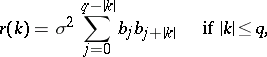 |
 |
Conversely, if the correlation function 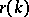 of a stationary process
of a stationary process 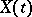 in discrete time
in discrete time 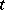 has the property that
has the property that  when
when 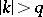 for some positive integer
for some positive integer 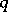 , then
, then  is a moving-average process of order
is a moving-average process of order  , that is, it has a representation of the form (1) where
, that is, it has a representation of the form (1) where  is a white noise (see, for example, [1]).
is a white noise (see, for example, [1]).
Along with the moving-average process of finite order 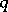 , which is representable in the form (1), there are two types of moving-average processes in discrete time of infinite order, namely: one-sided moving-average processes, having a representation of the form
, which is representable in the form (1), there are two types of moving-average processes in discrete time of infinite order, namely: one-sided moving-average processes, having a representation of the form
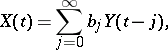 | (2) |
where  denotes white noise and the series on the right-hand side converges in mean-square (so that
denotes white noise and the series on the right-hand side converges in mean-square (so that  ), and also more general two-sided moving-average processes, of the form
), and also more general two-sided moving-average processes, of the form
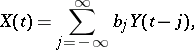 | (3) |
where 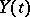 denotes white noise and
denotes white noise and 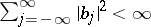 . The class of two-sided moving-average processes coincides with that of stationary processes
. The class of two-sided moving-average processes coincides with that of stationary processes 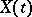 having spectral density
having spectral density 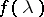 , while the class of one-sided moving-average processes coincides with that of processes having spectral density
, while the class of one-sided moving-average processes coincides with that of processes having spectral density 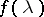 such that
such that
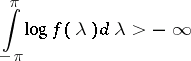 |
A continuous-time stationary process 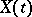 ,
, 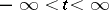 , is called a one-sided or two-sided moving-average process if it has the form
, is called a one-sided or two-sided moving-average process if it has the form
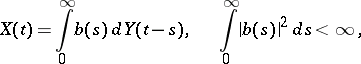 |
or
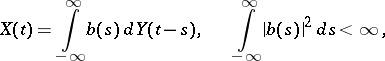 |
respectively, where 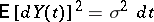 , that is,
, that is, 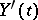 is a generalized white noise process. The class of two-sided moving-average processes in continuous time coincides with that of stationary processes
is a generalized white noise process. The class of two-sided moving-average processes in continuous time coincides with that of stationary processes 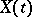 having spectral density
having spectral density 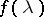 , while the class of one-sided moving-average processes in continuous time coincides with that of processes having spectral density
, while the class of one-sided moving-average processes in continuous time coincides with that of processes having spectral density 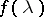 such that
such that
 |
References
| [1] | T.M. Anderson, "The statistical analysis of time series" , Wiley (1971) |
| [2] | A.N. Kolmogorov, "Stationary sequences in Hilbert space" T. Kailath (ed.) , Linear Least-Squares Estimation , Benchmark Papers in Electric Engin. Computer Sci. , 17 , Dowden, Hutchington & Ross (1977) pp. 66–89 (Translated from Russian) |
| [3] | J.L. Doob, "Stochastic processes" , Wiley (1953) |
| [4] | K. Karhunun, "Ueber lineare Methoden in der Wahrscheinlichkeitsrechnung" Ann. Acad. Sci. Fennicae Ser. A. Math. Phys. , 37 (1947) |
| [5] | Yu.A. Rozanov, "Stationary random processes" , Holden-Day (1967) (Translated from Russian) |
Comments
Both auto-regressive processes (cf. Auto-regressive process) and moving-average processes are special cases of so-called ARMA processes, i.e. auto-regressive moving-average processes (cf. Mixed autoregressive moving-average process), which are of great importance in the study of time series.
Moving-average process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Moving-average_process&oldid=12234