Irregular boundary point
A point  on the boundary
on the boundary  of a domain
of a domain  at which there is a continuous boundary function
at which there is a continuous boundary function  on
on  such that the Perron–Wiener–Brélot generalized solution (cf. Perron method) of the Dirichlet problem,
such that the Perron–Wiener–Brélot generalized solution (cf. Perron method) of the Dirichlet problem,  , does not take the boundary value
, does not take the boundary value  at
at  , i.e. either the limit
, i.e. either the limit
 |
does not exist, or it does not coincide with 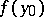 . For domains
. For domains 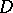 in the plane every isolated point of the boundary
in the plane every isolated point of the boundary 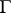 is irregular. In the case of a domain
is irregular. In the case of a domain 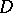 in a Euclidean space
in a Euclidean space 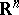 ,
, 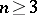 , it was H. Lebesgue who first discovered that the vertex of a very acute angle in
, it was H. Lebesgue who first discovered that the vertex of a very acute angle in 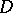 is an irregular boundary point. E.g., the coordinate origin
is an irregular boundary point. E.g., the coordinate origin 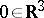 is an irregular boundary point if the boundary of the domain has, in a neighbourhood of
is an irregular boundary point if the boundary of the domain has, in a neighbourhood of  , the shape of the entering acute angle obtained by rotating the curve
, the shape of the entering acute angle obtained by rotating the curve 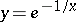 ,
, 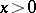 , around the positive
, around the positive  -axis (Lebesgue spine). The generalized solution of the Dirichlet problem does not take the boundary value
-axis (Lebesgue spine). The generalized solution of the Dirichlet problem does not take the boundary value 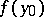 at an irregular boundary point if
at an irregular boundary point if 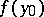 is the least upper or greatest lower bound of the values of
is the least upper or greatest lower bound of the values of 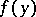 on
on 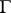 ; the classical solution does not exist in this case. The set of irregular boundary points is thin, in a certain sense: it has type
; the classical solution does not exist in this case. The set of irregular boundary points is thin, in a certain sense: it has type 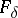 , is a polar set and has zero capacity. See also Barrier; Regular boundary point.
, is a polar set and has zero capacity. See also Barrier; Regular boundary point.
References
| [1] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
| [2] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
Comments
See [a2] for an additional classical reference, and [a1] for irregular points in axiomatic potential theory.
References
| [a1] | L.L. Helms, "Introduction to potential theory" , Wiley (1969) (Translated from German) |
| [a2] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
Irregular boundary point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Irregular_boundary_point&oldid=12226