Complete operator
A generalized wave operator, i.e. a partially isometric operator defined by
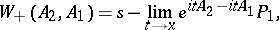 |
where 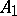 and
and 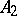 are self-adjoint operators on a separable Hilbert space
are self-adjoint operators on a separable Hilbert space 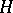 ,
, 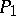 is an ortho-projector into
is an ortho-projector into 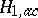 , and such that
, and such that
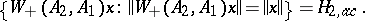 |
Here 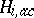 ,
, 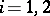 , is the set of all elements
, is the set of all elements  that are spectrally absolutely continuous with respect to
that are spectrally absolutely continuous with respect to 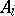 , i.e. for which the spectral measure
, i.e. for which the spectral measure 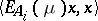 of a set
of a set 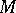 is absolutely continuous with respect to the Lebesgue measure
is absolutely continuous with respect to the Lebesgue measure 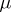 .
.
If the operator 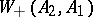 , or the analogously defined operator
, or the analogously defined operator 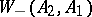 , exists and is complete, the
, exists and is complete, the 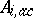 (the parts of the operators
(the parts of the operators 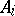 on
on 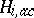 ) are unitarily equivalent. If
) are unitarily equivalent. If 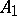 and
and 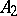 are self-adjoint operators on
are self-adjoint operators on 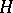 and
and 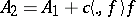 , where
, where 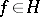 and
and  is real, then
is real, then 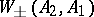 and
and 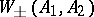 exist and are complete.
exist and are complete.
References
| [1] | T. Kato, "Perturbation theory for linear operators" , Springer (1966) pp. Chapt. X Sect. 3 |
Comments
An ortho-projector is usually called and orthogonal projector in the West.
An operator 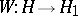 is partially isometric if there is a closed linear subspace
is partially isometric if there is a closed linear subspace 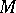 of
of 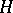 such that
such that  for
for 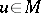 and
and 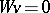 for
for 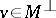 , the orthogonal complement of
, the orthogonal complement of  ; the set
; the set 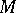 is called the initial set of
is called the initial set of 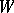 and
and  the final set of
the final set of 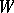 .
.
Complete operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_operator&oldid=12208