Schur multiplicator

Schur multiplier, of a group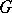

The cohomology group 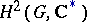, where 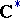is the multiplicative group of complex numbers with trivial 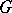-action. The Schur multiplicator was introduced by I. Schur [1] in his work on finite-dimensional complex projective representations of a group (cf. Projective representation). If 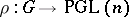is such a representation, then 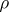can be interpreted as a mapping 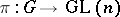such that

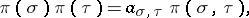where 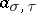is a -cocycle with values in 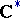. In particular, the projective representation 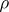is the projectivization of a linear representation 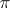if and only if the cocycle 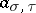determines the trivial element of the group 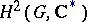. If 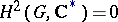, then 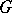is called a closed group in the sense of Schur. If 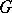is a finite group, then there exist natural isomorphisms

Let 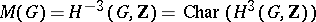. If a central extension

(*)

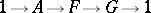of a finite group 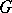is given, then there is a natural mapping 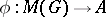whose image coincides with 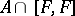. This mapping 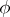coincides with the mapping 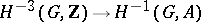induced by the cup-product with the element of 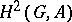defined by the extension (*). Conversely, for any subgroup 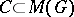there is an extension (*) such that 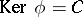. If 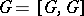, then the extension (*) is uniquely determined by the homomorphism 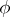. If 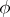is a monomorphism, then any projective representation of 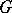is induced by some linear representation of .

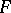References

[1]	I. Schur, "Ueber die Darstellung der endlichen Gruppen durch gebrochene lineare Substitutionen" J. Reine Angew. Math. , 127 (1904) pp. 20–50
[2]	S. MacLane, "Homology" , Springer (1975)

References

[a1]	G. Gruenberg, "Cohomological topics in group theory" , Lect. notes in math. , 143 , Springer (1970)
[a2]	C.W. Curtis, I. Reiner, "Methods of representation theory" , I , Wiley (Interscience) (1981)