Stirling interpolation formula

The half-sum of the Gauss interpolation formula for forward interpolation with respect to the nodes 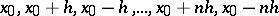at the point :

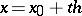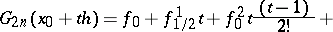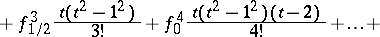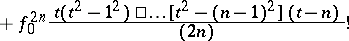and Gauss' formula of the same order for backward interpolation with respect to the nodes :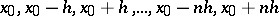

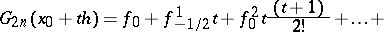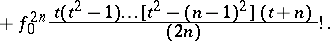Using the notation

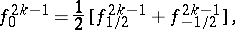Stirling's interpolation formula takes the form:

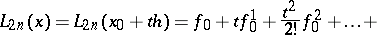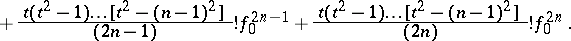For small 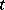, Stirling's interpolation formula is more exact than other interpolation formulas.

References

[1]	I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian)

Comments

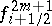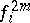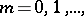
The central differences and ( 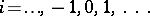) are defined recursively from the (tabulated values) 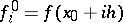by the formulas

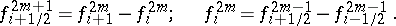References

[a1]	F.B. Hildebrand, "Introduction to numerical analysis" , Dover, reprint (1987) pp. 139