Graded module

A module that can be represented as the direct sum of its submodules (the index runs through all integers; some of the submodules may be trivial). A module is called positively graded if for all , and negatively graded if for all . The non-zero elements of are called homogeneous elements of degree . 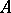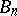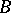A submodule of a graded module is said to be homogeneous if it can be decomposed into a direct sum of submodules such that for any integer ; is then a graded module. If 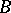is a homogeneous submodule of a graded module 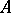, then the quotient module is also a graded module, i.e. , where 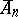is the image of the submodule under the natural homomorphism , 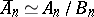. Graded modules are extensively used in homological algebra.

References

[1]	H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956)

Comments

A linear mapping between graded modules is a graded morphism if it respects the degree of homogeneous elements. The category of graded modules and graded morphisms is a Grothendieck category. Gradations by arbitrary groups may be introduced in a similar way. The gradations by the integers play an important role in the theory of projective algebraic varieties or schemes.

References

[a1]	C. Nâstâsescu, F. van Oystaeyen, "Graded ring theory" , North-Holland (1982)