Finitary verifiability
One of the non-classical interpretations of logical formulas proposed with the aim of making precise the program suggested by A.N. Kolmogorov of interpreting statements of intuitionistic logic as a calculus of problems.
Kolmogorov [1] expressed the idea that as well as traditional logic, which systematizes a scheme of proofs of theoretical truths, there is also possible a logic systematization of a scheme of solutions of problems. Without making the concept of a problem precise, one can still look at some concrete problems, for example:
1) to find four natural numbers  that satisfy
that satisfy  ,
, 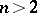 ;
;
2) to prove that the Fermat great theorem is false;
3) on the assumption that 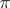 can be expressed in the form
can be expressed in the form  , where
, where 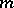 and
and  are integers, to find a similar expression for
are integers, to find a similar expression for  .
.
One can also define in a natural way the following operations on problems. If 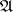 and
and 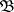 are problems, then
are problems, then  denotes the problem "solve both the problems A and B" ;
denotes the problem "solve both the problems A and B" ; 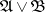 denotes "solve at least one of A or B" ;
denotes "solve at least one of A or B" ; 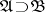 denotes "assuming that a solution of A is given, find a solution of B (that is, reduce B to A)" ;
denotes "assuming that a solution of A is given, find a solution of B (that is, reduce B to A)" ; 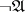 denotes "assuming that a solution of A is given, arrive at a contradiction" .
denotes "assuming that a solution of A is given, arrive at a contradiction" .
If one substitutes any problems for the variables in a propositional formula constructed from variables  by means of the logical connectives
by means of the logical connectives  ,
, 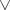 ,
,  ,
,  , then in accordance with the operations indicated one obtains some problem. A formula is called verifiable if there is a general method enabling one to solve any problem obtained in this way from the given formula. All formulas that are derivable in intuitionistic propositional calculus turn out to be verifiable in this sense. At the same time the formula
, then in accordance with the operations indicated one obtains some problem. A formula is called verifiable if there is a general method enabling one to solve any problem obtained in this way from the given formula. All formulas that are derivable in intuitionistic propositional calculus turn out to be verifiable in this sense. At the same time the formula  , which expresses the classical law of the excluded middle, cannot be verifiable, since if it were, that would mean that there would be a general method making it possible to obtain for every problem either a solution of it or a way of leading to a contradiction from the assumption that there is a solution of it.
, which expresses the classical law of the excluded middle, cannot be verifiable, since if it were, that would mean that there would be a general method making it possible to obtain for every problem either a solution of it or a way of leading to a contradiction from the assumption that there is a solution of it.
This description of the interpretation of logical formulas is not sufficiently strict, and such concepts as a "problem" , a "solution of a problem" and a "general method" need to be made precise. One way of doing so is the concept of finitary verifiability, proposed by Yu.T. Medvedev .
A finitary problem is a problem with as solution an element of some non-empty finite collection 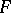 of admissible possibilities that are known beforehand. So, a finitary problem can be regarded as an ordered pair
of admissible possibilities that are known beforehand. So, a finitary problem can be regarded as an ordered pair  , where
, where  is the finite set of admissible possibilities for
is the finite set of admissible possibilities for 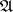 and
and 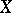 is the set of solutions
is the set of solutions  . If
. If  , one writes
, one writes  ,
, 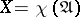 . Let
. Let  and
and 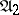 be arbitrary finitary problems with
be arbitrary finitary problems with
 |
Operations on finitary problems are defined as follows. For the conjunction  one sets
one sets
 |
where  denotes the Cartesian product of
denotes the Cartesian product of  and
and 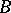 , that is, the set of all ordered pairs
, that is, the set of all ordered pairs  ,
, 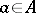 ,
,  . For the disjunction
. For the disjunction  one sets
one sets
 |
where  denotes the disjunctive union of
denotes the disjunctive union of 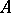 and
and 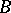 , that is, the set-theoretic union of
, that is, the set-theoretic union of 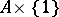 and
and 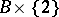 . For the implication
. For the implication 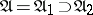 one sets
one sets 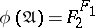 — the set of all mappings of
— the set of all mappings of 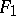 to
to  , and one lets
, and one lets  be the set of those
be the set of those 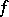 in
in 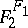 for which
for which  . The negation
. The negation 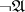 of
of 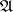 is defined as the problem
is defined as the problem  , where
, where  is a fixed problem with an empty solution set (all the constructions from now on are independent of the concrete choice of such a problem).
is a fixed problem with an empty solution set (all the constructions from now on are independent of the concrete choice of such a problem).
Substituting finitary problems 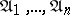 for the variables
for the variables  in a propositional formula
in a propositional formula  , one obtains a composite problem
, one obtains a composite problem 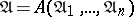 . Here
. Here 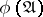 is determined only by the sets
is determined only by the sets 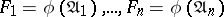 and does not depend on
and does not depend on 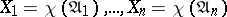 . For fixed sets
. For fixed sets  , the choice of different sets
, the choice of different sets  ,
, 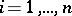 , will correspond to different problems
, will correspond to different problems  with the same set
with the same set  and, generally speaking, different sets
and, generally speaking, different sets 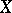 . If there is an element of
. If there is an element of 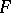 belonging to all such
belonging to all such  , then one says that the formula
, then one says that the formula 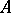 is solvable on the system of sets
is solvable on the system of sets  . If the formula
. If the formula  is solvable on every system of finite sets
is solvable on every system of finite sets 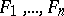 , then it is called generally solvable or finitarily verifiable. This definition has a transparent meaning: A formula
, then it is called generally solvable or finitarily verifiable. This definition has a transparent meaning: A formula  is finitarily verifiable if one can solve every problem
is finitarily verifiable if one can solve every problem  if one knows just the sets of admissible solutions of the problems
if one knows just the sets of admissible solutions of the problems  .
.
The set  of all finitarily-verifiable propositional formulas is closed relative to derivability in intuitionistic propositional calculus, and contains all formulas that are derivable in that calculus. Thus,
of all finitarily-verifiable propositional formulas is closed relative to derivability in intuitionistic propositional calculus, and contains all formulas that are derivable in that calculus. Thus, 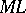 is an intermediate (or super-intuitionistic, or super-constructive) logic, called the Medvedev logic. This logic contains formulas that are not derivable in intuitionistic logic (such as, for example,
is an intermediate (or super-intuitionistic, or super-constructive) logic, called the Medvedev logic. This logic contains formulas that are not derivable in intuitionistic logic (such as, for example, 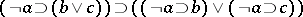 ). The Medvedev logic has the disjunctive property: If a formula of the form
). The Medvedev logic has the disjunctive property: If a formula of the form  is finitarily verifiable, then at least one of
is finitarily verifiable, then at least one of 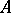 and
and 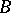 is finitarily verifiable. If a propositional formula does not contain any of the logical symbols
is finitarily verifiable. If a propositional formula does not contain any of the logical symbols  ,
, 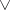 or
or  , then it is finitarily verifiable if and only if it is derivable in intuitionistic propositional calculus. All finitarily-verifiable formulas are derivable in classical propositional calculus; at the same time, for example, the classically-derivable formula
, then it is finitarily verifiable if and only if it is derivable in intuitionistic propositional calculus. All finitarily-verifiable formulas are derivable in classical propositional calculus; at the same time, for example, the classically-derivable formula  is not finitarily verifiable. Characterizations of the Medvedev logic in terms of algebraic models have been obtained. The concept of finitary verifiability can be extended in various ways to predicate formulas.
is not finitarily verifiable. Characterizations of the Medvedev logic in terms of algebraic models have been obtained. The concept of finitary verifiability can be extended in various ways to predicate formulas.
References
| [1] | A. Kolmogorov, "Zur Deutung der intuitionistischen Logik" Math. Z. , 35 (1932) pp. 58–65 |
| [2a] | Yu.T. Medvedev, "Interpretation of logical formulas by means of finite problems" Soviet Math. Dokl. , 7 : 4 (1966) pp. 857–860 Dokl. Akad. Nauk SSSR , 142 : 5 (1962) pp. 1015–1018 |
| [2b] | Yu.T. Medvedev, "Finite problems" Soviet Math. Dokl. , 3 (1962) pp. 227–230 Dokl. Akad. Nauk SSSR , 169 : 1 (1966) pp. 20–23 |
Finitary verifiability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finitary_verifiability&oldid=12156