Risk of a statistical procedure
A characteristic giving the mean loss of an experimenter in a problem of statistical decision making and thus defining the quality of the statistical procedure under consideration.
Suppose that one has to make a decision  in a measurable decision space
in a measurable decision space  with respect to a parameter
with respect to a parameter  on the basis of a realization of a random variable
on the basis of a realization of a random variable  with values in a sampling space
with values in a sampling space  ,
,  . Further, let the loss of a statistician caused by making the decision
. Further, let the loss of a statistician caused by making the decision  when the random variable
when the random variable  follows the law
follows the law  be
be 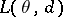 , where
, where 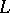 is some loss function given on
is some loss function given on 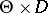 . In this case, if the statistician uses a non-randomized decision function
. In this case, if the statistician uses a non-randomized decision function 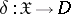 in the problem of decision making, then as a characteristic of this function
in the problem of decision making, then as a characteristic of this function  the function
the function
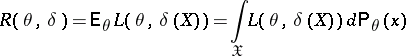 |
is used. It is called the risk function or, simply, the risk, of the statistical procedure based on the decision function  with respect to the loss
with respect to the loss  .
.
The concept of risk allows one to introduce a partial order on the set  of all non-randomized decision functions, since it is assumed that between two different decision functions
of all non-randomized decision functions, since it is assumed that between two different decision functions 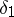 and
and  one should prefer
one should prefer 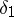 if
if  uniformly over all
uniformly over all 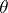 .
.
If the decision function 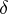 is randomized, the risk of the statistical procedure is defined by the formula
is randomized, the risk of the statistical procedure is defined by the formula
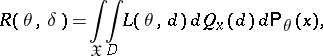 |
where  is the family of Markov transition probability distributions determining the randomization procedure.
is the family of Markov transition probability distributions determining the randomization procedure.
References
| [1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
| [2] | N.N. Chentsov, "Statistical decision rules and optimal inference" , Amer. Math. Soc. (1982) (Translated from Russian) |
| [3] | A. Wald, "Statistical decision functions" , Wiley (1950) |
Risk of a statistical procedure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Risk_of_a_statistical_procedure&oldid=12130