Least-favourable distribution
An a priori distribution maximizing the risk function in a statistical problem of decision making.
Suppose that, based on a realization of a random variable 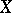 with values in a sample space
with values in a sample space 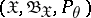 ,
, 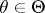 , one has to choose a decision
, one has to choose a decision 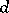 from a decision space
from a decision space 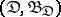 ; it is assumed here that the unknown parameter
; it is assumed here that the unknown parameter 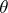 is a random variable taking values in a sample space
is a random variable taking values in a sample space 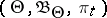 ,
, 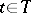 . Let
. Let 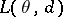 be a function representing the loss incurred by adopting the decision
be a function representing the loss incurred by adopting the decision 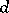 if the true value of the parameter is
if the true value of the parameter is 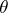 . An a priori distribution
. An a priori distribution 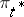 from the family
from the family 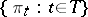 is said to be least favourable for a decision
is said to be least favourable for a decision 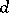 in the statistical problem of decision making using the Bayesian approach if
in the statistical problem of decision making using the Bayesian approach if
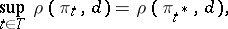 |
where
 |
is the risk function, representing the mean loss incurred by adopting the decision 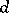 . A least-favourable distribution
. A least-favourable distribution 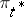 makes it possible to calculate the "greatest" (on the average) loss
makes it possible to calculate the "greatest" (on the average) loss 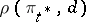 incurred by adopting
incurred by adopting 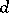 . In practical work one is guided, as a rule, not by the least-favourable distribution, but, on the contrary, strives to adopt a decision that would safeguard one against maximum loss when
. In practical work one is guided, as a rule, not by the least-favourable distribution, but, on the contrary, strives to adopt a decision that would safeguard one against maximum loss when 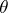 varies; this implies a search for a minimax decision
varies; this implies a search for a minimax decision 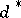 minimizing the maximum risk, i.e.
minimizing the maximum risk, i.e.
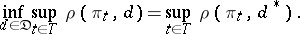 |
When testing a composite statistical hypothesis against a simple alternative, within the Bayesian approach, one defines a least-favourable distribution with the aid of Wald reduction, which may be described as follows. Suppose that, based on a realization of a random variable 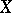 , one has to test a composite hypothesis
, one has to test a composite hypothesis 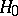 , according to which the distribution law of
, according to which the distribution law of 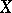 belongs to a family
belongs to a family 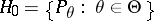 , against a simple alternative
, against a simple alternative 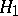 , according to which
, according to which 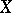 obeys a law
obeys a law 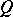 ; let
; let
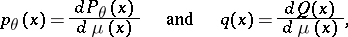 |
where 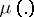 is a
is a  -finite measure on
-finite measure on 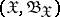 and
and 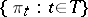 is a family of a priori distributions on
is a family of a priori distributions on 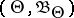 . Then, for any
. Then, for any 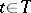 , the composite hypothesis
, the composite hypothesis 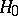 can be associated with a simple hypothesis
can be associated with a simple hypothesis 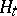 , according to which
, according to which 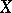 obeys the probability law with density
obeys the probability law with density
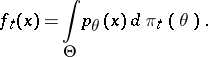 |
By the Neyman–Pearson lemma for testing a simple hypothesis 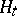 against a simple alternative
against a simple alternative 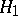 , there exists a most-powerful test, based on the likelihood ratio. Let
, there exists a most-powerful test, based on the likelihood ratio. Let 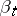 be the power of this test (cf. Power of a statistical test). Then the least-favourable distribution is the a priori distribution
be the power of this test (cf. Power of a statistical test). Then the least-favourable distribution is the a priori distribution 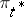 from the family
from the family 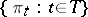 such that
such that 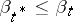 for all
for all 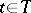 . The least-favourable distribution has the property that the density
. The least-favourable distribution has the property that the density 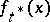 of
of 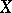 under the hypothesis
under the hypothesis 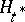 is the "least distant" from the alternative density
is the "least distant" from the alternative density 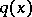 , i.e. the hypothesis
, i.e. the hypothesis 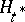 is the member of the family
is the member of the family 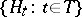 "nearest" to the rival hypothesis
"nearest" to the rival hypothesis 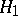 . See Bayesian approach.
. See Bayesian approach.
References
| [1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
| [2] | S. Zachs, "Theory of statistical inference" , Wiley (1971) |
Least-favourable distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Least-favourable_distribution&oldid=12123