Analytic theory of differential equations

The branch of the theory of ordinary differential equations in which the solutions are studied from the point of view of the theory of analytic functions. A typical formulation of a problem in the analytic theory of differential equations is this: Given a certain class of differential equations, the solutions of which are all analytic functions of one variable, find the specific properties of the analytic functions that are solutions of this class of equations. In this wide sense, the analytic theory of differential equations includes the theory of algebraic functions, the theory of Abelian integrals, the theory of special functions, etc. Special functions — Bessel functions, Airy functions, Legendre functions, Laguerre functions, Hermite functions (cf. Hermite function), Chebyshev functions (cf. Chebyshev function), Whittaker functions, Weber functions (cf. Weber function), Mathieu functions, hypergeometric functions (cf. Hypergeometric function), Sonin functions and many other functions — are solutions of linear differential equations with analytic coefficients.

Linear theory.

Consider a system of equations in matrix notation:

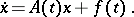(1)

1) Let the matrices 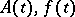be holomorphic in a region 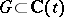, where 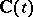is the complex 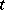-plane. Any solution of the system (1) will then be analytic in 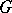(but will not, in general, be single-valued if 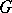is not simply-connected). It is assumed that 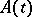is meromorphic in 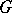, and one considers the homogeneous system

(2)

(The matrix is called holomorphic (meromorphic) in if all its elements are holomorphic (meromorphic) in 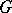.) A point 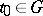is called a pole of the matrix 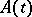of order if, in a given neighbourhood of this point,

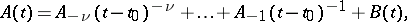where 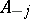are constant matrices, 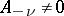, and the matrix 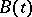is holomorphic at 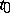. A pole 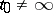of order is called a regular singular point if 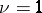and an irregular singular point if 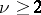. The case 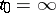is reduced to the case by the change of variables 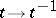. In what follows, .

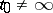2) Let 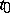be a pole of 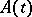. Then there exists a fundamental matrix 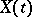for the system (2) of the form

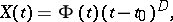(3)

where 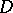is a constant matrix, 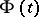is holomorphic if 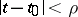where 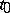is a regular singular point, and 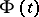is holomorphic if 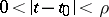where 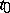is an irregular singular point, for some 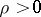. (Here, 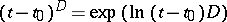, by definition.) For a regular singular point the matrix 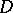can be expressed in terms of 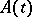in an explicit form [1], [2]; this is not the case for irregular singular points.

A similar classification of singular points is introduced for differential equations of order with meromorphic coefficients. Differential equations and differential systems all singular points of which are regular are known as Fuchsian differential equations (systems). The general form of 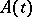for such a system is:

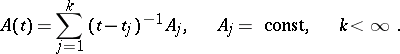An example of a Fuchsian differential equation is the hypergeometric equation.

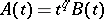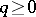3) Let where is an integer and let 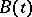be holomorphic at 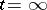( 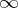is an irregular singular point 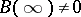if ). If 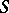is a sufficiently narrow sector of the form 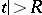, , 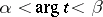then there exists a fundamental matrix of the form

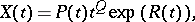(4)

where 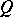is a constant matrix, 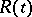is a diagonal matrix whose elements are polynomials in 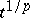, is an integer and

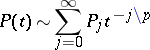as 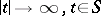. The plane 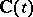is subdivided into a finite number of sectors, and in of them there exists a fundamental matrix of the form (4) ([3], [4]; see also [1], [2]).

4) As a result of analytic continuation along a closed path 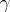the fundamental matrix 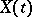is multiplied by 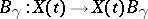, where 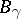is a constant matrix; one obtains the monodromy group of the differential equation. I.A. Lappo-Danilevskii [5] has studied the problem of Riemann: Let 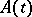be a rational function of 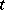and let the singularities of the fundamental matrix 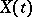be known, find .

5) Let the function be a conformal mapping of the upper half-plane 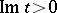onto the interior of a polygon, the boundary of which consists of a finite number of segments of straight lines and circular arcs. The function 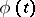will then satisfy the Schwarz equation:

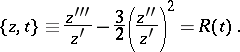(5)

where is a rational function, and the equation

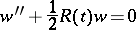(6)

is Fuchsian. Any solution of equation (5) may be represented in the form 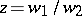, where 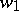and 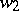are linearly independent solutions of equation (6). Let 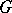be an infinite discrete group and let 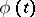be an automorphic function of , then 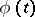can be represented as 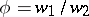, where 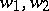are linearly independent solutions of equation (6) and 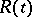is some algebraic function.

Non-linear theory.

1) Consider the Cauchy problem:

(7)

where , .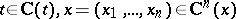

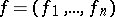Cauchy's theorem: Let the function 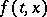be holomorphic in 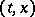in a region 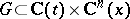and let the point 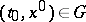. Then there exists a 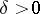such that in the domain 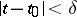there exists a solution 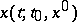of the Cauchy problem (7), which is unique and holomorphic.

An analytic continuation of the solution will also be a solution of the system (7), but the function obtained as a result of the continuation may have singularities and, in the general case, is a many-valued function of 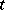. The problems which arise are: What singularities may this function have and how can one construct the general solution? In the linear case these questions have been conclusively answered. In the non-linear case the situation is much more complicated and has not been fully clarified even when the 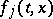are rational functions of .

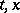2) Consider the differential equation:

(8)

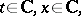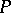where and and 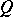are holomorphic functions of 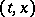in a certain region 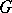. A point 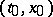is called an (essentially) singular point of equation (8) if 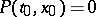, 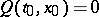. Below the structure of the solutions in a neighbourhood of a singular point of the equation is clarified. Develop 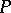and 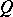into Taylor series:

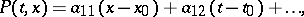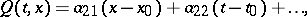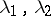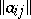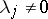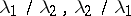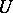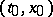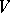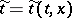and let be the eigen values of the matrix . The following theorem holds. Let and let none of the numbers be either a non-negative integer or a real negative number. Then there exists a neighbourhood of the point , a neighbourhood of the point , and functions and 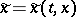such that the mapping 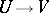defined by these functions is biholomorphic, and the differential equation (8) in the new variables assumes the form [6]:

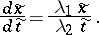All solutions of equation (8) in the new variables are written in the form 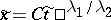and 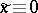. Thus, a singular point of the equation is a branching point of infinite order for all solutions of equation (8) (except for the trivial solutions). The singular points of the solution which coincide with the singular points of the equation are called stationary. As distinct from the linear case, the solution of a non-linear equation may have singular points not only at the singular points of the equation; such singular points of the solution are called movable. Painlevé's theorem is valid: The solutions of the equation

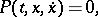where 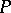is a polynomial in and 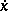with holomorphic coefficients in 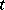, has no movable transcendental singular points [7].

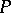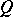If, in equation (8), and are polynomials in 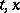, then, in view of Painlevé's theorem, all movable singular points are algebraic. On substituting 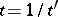, , 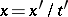equation (8) assumes the form

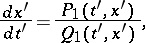where 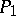and 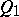are polynomials. Let 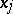be the roots of the equation 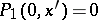. The points 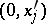are called infinitely-remote singular points of equation (8); the structure of the solutions in a neighbourhood of these points is described by the theorem quoted above [6].

Let 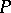and 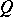be polynomials of degree . Since 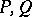are defined by their coefficients and the pair 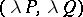defines the same equation, one obtains a one-to-one correspondence between equations (8) and the points of the complex projective space 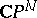, 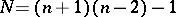. The following theorem is valid: If some set of measure zero is removed from 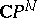, the remaining equations (8) will have the following property: All solutions 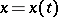are everywhere dense in 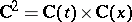[8].

3) Consider the autonomous system

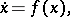(9)

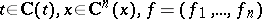. A point 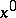will then be a singular point of the system (9) if 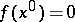. Poincaré's theorem is valid: Let 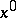be a singular point of the autonomous system (9). Also let a) the elementary divisors of the Jacobi matrix 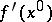be prime divisors; and b) the eigen values 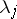of this matrix lie on one side of some straight line in 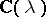passing through the coordinate origin. Then there exists neighbourhoods 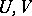of the points 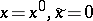and a biholomorphic mapping 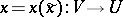such that the system (9) expressed in the variable 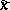assumes the form [9]:

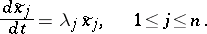If only condition a) is satisfied, it is possible, by using a transformation 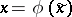, where 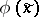is a formal power series, to convert system (9) in a neighbourhood of a singular point into a system which can be integrated in quadratures [9], [10]. However, the convergence of these series has been proved on assumptions close to a) and b). If the function and the transformation 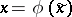are real for real 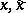, a theorem similar to the theorem of Poincaré has been proved [11]. The structure of the solutions of the autonomous system (9) in general, where 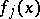are polynomials and 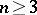, has not yet (1970s) been studied.

References

[1]	E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955)
[2]	W. Wazov, "Asymptotic expansions for ordinary differential equations" , Interscience (1965)
[3]	G.D. Birkhoff, "Singular points of ordinary linear differential equations" Trans. Amer. Math. Soc. , 10 (1909) pp. 436–470
[4]	W.J. Trjitzinsky, "Analytic theory of linear differential equations" Acta Math. , 62 (1934) pp. 167–226
[5]	J.A. Lappo-Danilevsky, "Mémoire sur la théorie des systèmes des équations différentielles linéaires" , Chelsea, reprint (1953)
[6]	L. Bieberbach, "Theorie der gewöhnlichen Differentialgleichungen auf funktionentheoretischer Grundlage dargestellt" , Springer (1965)
[7]	V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian)
[8]	M.G. Khudai-Verenov, "On a property of solutions of a differential equation" Mat. Sb. , 56 (98) : 3 (1962) pp. 301–308 (In Russian)
[9]	V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)
[10]	A.D. Bryuno, "Local methods in nonlinear differential equations" , Springer (1989) (Translated from Russian)
[11]	C.L. Siegel, "Ueber die Normalform analytischer Differentialgleichungen in der Nähe einer Gleichgewichtslösung" Nachrichten Akad. Wissenschaft. Göttingen (1952) pp. 21–30
[12]	H. Poincaré, , Oeuvres de H. Poincaré , 3 , Gauthier-Villars (1916–1965)
[13]	L.R. Ford, "Automorphic functions" , Chelsea, reprint (1951)

Comments

The Riemann monodromy problem mentioned above is of great importance in the modern theory of completely integrable or soliton equations. Cf. Soliton.

References

[a1]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956)
[a2]	E. Hille, "Ordinary differential equations in the complex domain" , Wiley (Interscience) (1976)