Wedge (in a vector space)
convex cone
A convex set in a vector space over an ordered field that is invariant with respect to the transformation 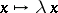 ,
, 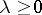 , that is, a set
, that is, a set 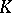 such that if
such that if 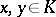 and
and 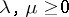 , then
, then 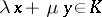 . A convex cone
. A convex cone 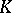 satisfying the condition: If
satisfying the condition: If 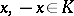 then
then 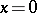 , is called a proper (convex) cone. Each proper cone induces in the vector space a quasi-order:
, is called a proper (convex) cone. Each proper cone induces in the vector space a quasi-order: 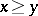 when
when 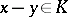 . A proper cone
. A proper cone 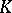 in a space
in a space 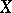 is called reproducing (or a domain of positivity) if
is called reproducing (or a domain of positivity) if 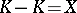 .
.
Comments
Open sets 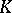 defined, as above, by the requirements that
defined, as above, by the requirements that 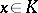 implies
implies 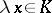 , for all
, for all 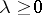 , and
, and 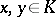 implies
implies 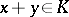 , are usually called (open) cones.
, are usually called (open) cones.
Let 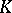 be an open cone in a real topological vector space
be an open cone in a real topological vector space 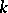 , let
, let 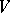 be the intersection of
be the intersection of 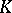 with a bounded open ball with centre at
with a bounded open ball with centre at 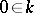 , and let
, and let 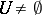 be an open set in
be an open set in 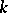 . Let
. Let
 |
be sets in the complexification of 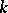 (
(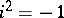 ). Then
). Then 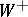 and
and 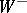 are called wedges (and
are called wedges (and 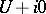 is their "edge" ). For a use of wedges in the theory of analytic continuation see Bogolyubov theorem.
is their "edge" ). For a use of wedges in the theory of analytic continuation see Bogolyubov theorem.
Wedge (in a vector space). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wedge_(in_a_vector_space)&oldid=12115