Scheme
A ringed space that is locally isomorphic to an affine scheme. More precisely, a scheme consists of a topological space 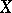 (the underlying space of the scheme) and a sheaf
(the underlying space of the scheme) and a sheaf 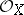 of commutative rings with a unit on
of commutative rings with a unit on 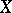 (the structure sheaf of the scheme); moreover, an open covering
(the structure sheaf of the scheme); moreover, an open covering 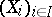 of
of 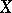 must exist such that
must exist such that 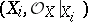 is isomorphic to the affine scheme
is isomorphic to the affine scheme 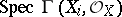 of the ring of sections of
of the ring of sections of 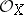 over
over 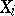 . A scheme is a generalization of the concept of an algebraic variety. For the history of the concept of a scheme, see [2], [3], [5].
. A scheme is a generalization of the concept of an algebraic variety. For the history of the concept of a scheme, see [2], [3], [5].
Basic concepts and properties.
Let 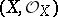 be a scheme. For every point
be a scheme. For every point 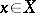 , the stalk
, the stalk 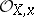 at
at  of the sheaf is a local ring; the residue field of this ring is denoted by
of the sheaf is a local ring; the residue field of this ring is denoted by 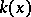 and is called the residue field of the point
and is called the residue field of the point  . As the topological properties of the scheme the properties of the underlying space
. As the topological properties of the scheme the properties of the underlying space 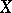 are considered (for example, quasi-compactness, connectedness, irreducibility). If
are considered (for example, quasi-compactness, connectedness, irreducibility). If 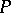 is a property of affine schemes (i.e. a property of rings), then one says that a scheme has property
is a property of affine schemes (i.e. a property of rings), then one says that a scheme has property 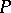 locally if any of its points has an open affine neighbourhood that has this property. The property of being locally Noetherian is an example of this (see Noetherian scheme). A scheme is regular if all its local rings are regular (cf. Regular ring (in commutative algebra)). Other schemes defined in the same way include normal and reduced schemes, as well as Cohen–Macaulay schemes.
locally if any of its points has an open affine neighbourhood that has this property. The property of being locally Noetherian is an example of this (see Noetherian scheme). A scheme is regular if all its local rings are regular (cf. Regular ring (in commutative algebra)). Other schemes defined in the same way include normal and reduced schemes, as well as Cohen–Macaulay schemes.
A morphism of schemes is a morphism between them as locally ringed spaces. In other words, a morphism 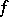 of a scheme
of a scheme 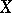 into a scheme
into a scheme 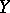 consists of a continuous mapping
consists of a continuous mapping  and a homomorphism of the sheaves of rings
and a homomorphism of the sheaves of rings 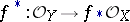 , where for any point
, where for any point 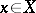 , the homomorphism of local rings
, the homomorphism of local rings 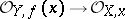 must map maximal ideals to maximal ideals. For any ring
must map maximal ideals to maximal ideals. For any ring 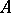 , the morphisms of
, the morphisms of 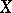 into
into 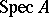 are in bijective correspondence with the ring homomorphisms
are in bijective correspondence with the ring homomorphisms 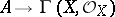 . For any point
. For any point 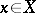 , its imbedding in
, its imbedding in 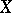 can also be considered as a morphism of schemes
can also be considered as a morphism of schemes 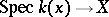 . An important property is the existence in the category of schemes of direct and fibre products (cf. Fibre product of objects in a category), which generalize the concept of the tensor product of rings. The underlying topological space of the product of two schemes
. An important property is the existence in the category of schemes of direct and fibre products (cf. Fibre product of objects in a category), which generalize the concept of the tensor product of rings. The underlying topological space of the product of two schemes 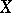 and
and 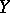 differs, generally speaking, from the product of the underlying spaces
differs, generally speaking, from the product of the underlying spaces 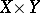 .
.
A scheme 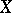 endowed with a morphism into a scheme
endowed with a morphism into a scheme 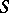 is called an
is called an 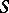 -scheme, or a scheme over
-scheme, or a scheme over 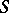 . A morphism
. A morphism 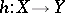 is called a morphism of
is called a morphism of 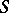 -schemes
-schemes 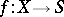 and
and 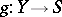 if
if 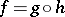 . Any scheme can be seen as a scheme over
. Any scheme can be seen as a scheme over 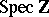 . A morphism of base change
. A morphism of base change 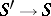 permits a transition from the
permits a transition from the 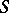 -scheme
-scheme 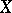 to the
to the 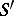 -scheme
-scheme 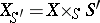 — the fibre product of
— the fibre product of  and
and 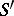 . If the underlying scheme
. If the underlying scheme 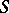 is the spectrum of a ring
is the spectrum of a ring 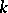 , then one also speaks of a
, then one also speaks of a 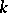 -scheme. A
-scheme. A 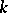 -scheme
-scheme 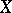 is called a
is called a 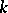 -scheme of finite type if a finite affine covering
-scheme of finite type if a finite affine covering 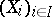 of
of 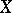 exists such that the
exists such that the  -algebras
-algebras 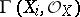 are generated by a finite number of elements. A scheme of finite type over a field, sometimes requiring separability and completeness, is usually called an algebraic variety. A morphism of
are generated by a finite number of elements. A scheme of finite type over a field, sometimes requiring separability and completeness, is usually called an algebraic variety. A morphism of 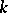 -schemes
-schemes 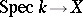 is called a rational point of the
is called a rational point of the 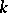 -scheme
-scheme 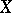 ; the set of such points is denoted by
; the set of such points is denoted by 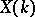 .
.
For an 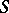 -scheme
-scheme 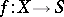 and a point
and a point 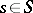 , the
, the 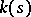 -scheme
-scheme 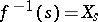 , obtained from
, obtained from 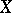 by a base change
by a base change 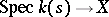 , is called a stalk (or fibre) of the morphism
, is called a stalk (or fibre) of the morphism 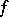 over
over  . If, instead of the field
. If, instead of the field 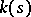 in this definition one takes its algebraic closure, then the concept of a geometric fibre is obtained. Thereby, the
in this definition one takes its algebraic closure, then the concept of a geometric fibre is obtained. Thereby, the 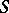 -scheme
-scheme 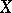 can be considered as a family of schemes
can be considered as a family of schemes 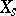 parametrized by the scheme
parametrized by the scheme 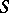 . Often, when speaking of families, it is also required that the morphism
. Often, when speaking of families, it is also required that the morphism 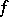 be flat (cf. Flat morphism).
be flat (cf. Flat morphism).
Concepts relating to schemes over 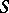 are often said to be relative, as opposed to the absolute concepts relating to schemes. In fact, for every concept that is used for schemes there is a relative variant. For example, an
are often said to be relative, as opposed to the absolute concepts relating to schemes. In fact, for every concept that is used for schemes there is a relative variant. For example, an 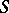 -scheme
-scheme 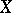 is said to be separated if the diagonal imbedding
is said to be separated if the diagonal imbedding 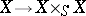 is closed; a morphism
is closed; a morphism 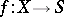 is said to be smooth if it is flat and all its geometric fibres are regular. Other morphisms defined in the same way include affine, projective, proper, finite, étale, non-ramified, finite-type, etc. A property of a morphism is said to be universal if it is preserved under any base change.
is said to be smooth if it is flat and all its geometric fibres are regular. Other morphisms defined in the same way include affine, projective, proper, finite, étale, non-ramified, finite-type, etc. A property of a morphism is said to be universal if it is preserved under any base change.
Cohomology of schemes.
Studies of schemes and related algebraic-geometric objects can often be divided into two problems — local and global. Local problems are usually linearized and their data are described by some coherent sheaf or by sheaf complexes. For example, in the study of the local structure of a morphism 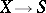 , the sheaves
, the sheaves 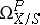 of relative differential forms (cf. Differential form) are of some importance. The global part is usually related to the cohomology of these sheaves (see, for example, deformation of an algebraic variety). Finiteness theorems are useful here, as are theorems on the vanishing of the cohomology spaces (see Kodaira theorem), duality, the Künneth formula, the Riemann–Roch theorem, etc.
of relative differential forms (cf. Differential form) are of some importance. The global part is usually related to the cohomology of these sheaves (see, for example, deformation of an algebraic variety). Finiteness theorems are useful here, as are theorems on the vanishing of the cohomology spaces (see Kodaira theorem), duality, the Künneth formula, the Riemann–Roch theorem, etc.
A scheme of finite type over a field 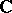 can also be considered as a complex analytic space. Using transcendental methods, it is possible to calculate the cohomology of coherent sheaves; it is more important, however, that it is possible to speak of the complex, or strong, topology on
can also be considered as a complex analytic space. Using transcendental methods, it is possible to calculate the cohomology of coherent sheaves; it is more important, however, that it is possible to speak of the complex, or strong, topology on 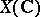 , the fundamental group, the Betti numbers, etc. The desire to find something similar for arbitrary schemes and the far-reaching arithmetical hypotheses put forward (see Zeta-function in algebraic geometry) have led to the construction of different topologies in the category of schemes, the best known of which is the étale topology (cf. Etale topology). This has made it possible to define the fundamental group of a scheme, other homotopy invariants, cohomology spaces with values in discrete sheaves, Betti numbers, etc. (see
, the fundamental group, the Betti numbers, etc. The desire to find something similar for arbitrary schemes and the far-reaching arithmetical hypotheses put forward (see Zeta-function in algebraic geometry) have led to the construction of different topologies in the category of schemes, the best known of which is the étale topology (cf. Etale topology). This has made it possible to define the fundamental group of a scheme, other homotopy invariants, cohomology spaces with values in discrete sheaves, Betti numbers, etc. (see 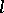 -adic cohomology; Weil cohomology; Motives, theory of).
-adic cohomology; Weil cohomology; Motives, theory of).
Construction of schemes.
In the construction of a concrete scheme one most frequently uses the concepts of an affine or projective spectrum (see Affine morphism; Projective scheme), including the definition of a subscheme by a sheaf of ideals. The construction of a projective spectrum makes it possible, in particular, to construct a monoidal transformation of schemes. Fibre products and glueing are also used in the construction of schemes. Less elementary constructions rely on the concept of a representable functor. By having at one's disposal a good concept of a family of objects parametrized by schemes, and by juxtaposing every scheme 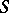 with a set
with a set 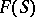 of families parametrized by
of families parametrized by 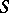 , a contravariant functor
, a contravariant functor 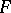 is obtained from the category of schemes into the category of sets (possibly with an additional structure). If the functor
is obtained from the category of schemes into the category of sets (possibly with an additional structure). If the functor 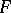 is representable, i.e. if a scheme
is representable, i.e. if a scheme 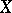 exists such that
exists such that 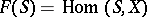 for any
for any 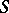 , then a universal family of objects parametrized by
, then a universal family of objects parametrized by 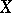 is obtained. The Picard scheme and Hilbert scheme are constructed in this way (see also Algebraic space; Moduli theory).
is obtained. The Picard scheme and Hilbert scheme are constructed in this way (see also Algebraic space; Moduli theory).
One other method of generating new schemes is transition to a quotient space by means of an equivalence relation on a scheme. As a rule, this quotient space exists as an algebraic space. A particular instance of this construction is the scheme of orbits  under the action of a group scheme
under the action of a group scheme 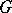 on a scheme
on a scheme 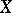 (see Invariants, theory of).
(see Invariants, theory of).
One of the generalizations of the concept of a scheme is a formal scheme, which may be understood to be the inductive limit of schemes with one and the same underlying topological space.
References
| [1] | A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" , I. Le langage des schémes , Springer (1971) |
| [2] | J. Dieudonné, "Cours de géométrie algébrique" , I , Presses Univ. France (1974) |
| [3] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
| [4] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [5] | I.V. Dolgachev, "Abstract algebraic geometry" J. Soviet Math. , 2 : 3 (1974) pp. 264–303 Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 10 (1972) pp. 47–112 |
Comments
In earlier terminology, e.g. the fundamental original book [1], the phrase pre-scheme was used for a scheme as defined above; and scheme referred to a separated scheme, i.e. a scheme such that the diagonal 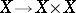 is closed.
is closed.
There are a large number of conditions, especially finiteness conditions, on morphisms between schemes that are considered. Some of these are as follows.
A morphism of schemes 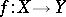 is a compact morphism (also called quasi-compact morphism) if there is an open covering of
is a compact morphism (also called quasi-compact morphism) if there is an open covering of 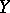 by affine sets
by affine sets 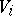 such that
such that 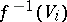 is compact for all
is compact for all 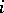 .
.
A morphism of schemes 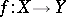 is a quasi-finite morphism if for every
is a quasi-finite morphism if for every 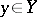 ,
, 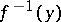 is a finite set.
is a finite set.
A morphism 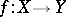 is a quasi-separated morphism if the diagonal morphism
is a quasi-separated morphism if the diagonal morphism 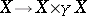 is compact.
is compact.
A morphism 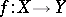 is a morphism locally of finite type if there exists a covering of
is a morphism locally of finite type if there exists a covering of 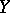 by open affine sets
by open affine sets 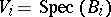 such that for each
such that for each 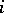 ,
, 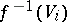 can be covered by open affine sets
can be covered by open affine sets 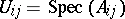 such that each
such that each 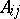 is a finitely-generated
is a finitely-generated 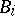 -algebra. If, in addition, finitely many
-algebra. If, in addition, finitely many 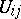 suffice (for each
suffice (for each  ), then
), then 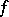 is a morphism of finite type.
is a morphism of finite type.
A morphism 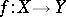 is a finite morphism if there exists a covering of
is a finite morphism if there exists a covering of 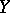 by open affine sets
by open affine sets 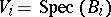 such that each
such that each 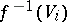 is affine, say
is affine, say 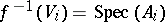 , and
, and 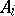 is a
is a 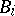 -algebra which is finitely generated as a
-algebra which is finitely generated as a 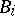 -module.
-module.
Let 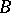 be an algebra over a ring
be an algebra over a ring 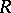 . The algebra
. The algebra 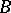 is said to be finitely presentable over
is said to be finitely presentable over 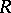 if it is isomorphic to a quotient
if it is isomorphic to a quotient 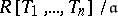 , where
, where  is a finitely-generated ideal in
is a finitely-generated ideal in 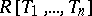 . If
. If 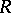 is Noetherian,
is Noetherian, 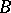 is finitely presentable if and only if
is finitely presentable if and only if 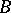 is of finite type (i.e. finitely generated as an algebra over
is of finite type (i.e. finitely generated as an algebra over 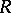 ).
).
Let 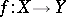 be a morphism of (pre-) schemes, and
be a morphism of (pre-) schemes, and 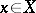 ,
, 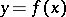 . Then
. Then 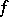 is said to be finitely presentable in
is said to be finitely presentable in  if there exists an open affine set
if there exists an open affine set 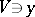 and an open affine set
and an open affine set 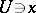 such that
such that 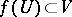 and such that the ring
and such that the ring  is a finitely-presentable
is a finitely-presentable 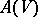 -algebra. The morphism
-algebra. The morphism 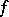 is said to be locally finitely presentable if it is finitely presentable in each point
is said to be locally finitely presentable if it is finitely presentable in each point  . If
. If 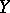 is locally Noetherian, a morphism
is locally Noetherian, a morphism 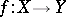 is locally finitely presentable if and only if it is locally of finite type. A morphism
is locally finitely presentable if and only if it is locally of finite type. A morphism 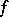 is finitely presentable if it is locally finitely presentable, quasi-compact and quasi-separated.
is finitely presentable if it is locally finitely presentable, quasi-compact and quasi-separated.
For some more important special conditions on morphisms of schemes and pre-schemes cf. Affine morphism; Smooth morphism (of schemes); Quasi-affine scheme; Separable mapping; Etale morphism; Proper morphism.
If 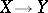 is a morphism of such-and-such-a-type, then one often says that
is a morphism of such-and-such-a-type, then one often says that 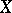 is a scheme of such-and-such-a-type over
is a scheme of such-and-such-a-type over 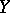 .
.
Scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Scheme&oldid=12110