Positive-definite form
An expression
 |
where  , which takes non-negative values for any real values
, which takes non-negative values for any real values  and vanishes only for
and vanishes only for  . Therefore, a positive-definite form is a quadratic form of special type. Any positive-definite form can be converted by a linear transformation to the representation
. Therefore, a positive-definite form is a quadratic form of special type. Any positive-definite form can be converted by a linear transformation to the representation
 |
In order that a form
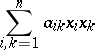 |
be positive definite, it is necessary and sufficient that  , where
, where
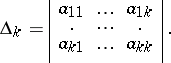 |
In any affine coordinate system, the distance of a point from the origin is expressed by a positive-definite form in the coordinates of the point.
A form
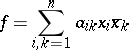 |
such that  and
and  for all values of
for all values of  and
and  only for
only for  is called a Hermitian positive-definite form.
is called a Hermitian positive-definite form.
The following concepts are related to the concept of a positive-definite form: 1) a positive-definite matrix  is a matrix such that
is a matrix such that  is a Hermitian positive-definite form; 2) a positive-definite kernel is a function
is a Hermitian positive-definite form; 2) a positive-definite kernel is a function 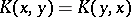 such that
such that
 |
for every function  with an integrable square; 3) a positive-definite function is a function
with an integrable square; 3) a positive-definite function is a function  such that the kernel
such that the kernel  is positive definite. By Bochner's theorem, the class of continuous positive-definite functions
is positive definite. By Bochner's theorem, the class of continuous positive-definite functions  with
with  coincides with the class of characteristic functions of distributions of random variables (cf. Characteristic function).
coincides with the class of characteristic functions of distributions of random variables (cf. Characteristic function).
Comments
A kernel that is semi-positive definite (non-negative definite) is one that satisfies  for all
for all  . Such a kernel is sometimes also simply called positive. However, the phrase "positive kernel" is also used for the weaker notion
. Such a kernel is sometimes also simply called positive. However, the phrase "positive kernel" is also used for the weaker notion  (almost-everywhere). A positive kernel
(almost-everywhere). A positive kernel  in the latter sense has at least one eigen value
in the latter sense has at least one eigen value  while a semi-positive definite kernel has all eigen values
while a semi-positive definite kernel has all eigen values  .
.
References
| [a1] | E. Lukacs, "Characteristic functions" , Griffin (1970) |
| [a2] | P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , Integral equations - a reference text , Noordhoff (1975) pp. Chapt. III, §3 (Translated from Russian) |
| [a3] | H. Hochstadt, "Integral equations" , Wiley (1973) pp. 255ff |
| [a4] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , I-II , Chelsea, reprint (1959) pp. Chapt. X (Translated from Russian) |
Positive-definite form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive-definite_form&oldid=12091