Babuska-Lax-Milgram theorem
Many boundary value problems for ordinary and partial differential equations can be posed in the following abstract variational form (cf. also Boundary value problem, ordinary differential equations; Boundary value problem, partial differential equations): Find 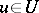 such that
such that
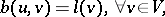 | (a1) |
where 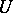 and
and 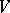 are real normed linear spaces (cf. Norm; Linear space),
are real normed linear spaces (cf. Norm; Linear space), 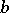 denotes a functional on
denotes a functional on 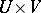 and
and 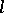 is an element in
is an element in 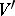 (the dual of
(the dual of 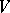 ).
).
The essential question here is what conditions can be imposed on 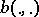 and on the normed spaces
and on the normed spaces 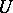 and
and 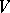 so that a unique solution to (a1) exists and depends continuously on the data
so that a unique solution to (a1) exists and depends continuously on the data 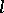 .
.
If 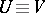 is a Hilbert space, P.D. Lax and A.N. Milgram [a1] have proved that for a bilinear continuous functional
is a Hilbert space, P.D. Lax and A.N. Milgram [a1] have proved that for a bilinear continuous functional 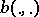 strong coerciveness (i.e., there is a
strong coerciveness (i.e., there is a 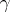 such that for all
such that for all 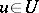 ,
, 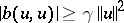 ) is a sufficient condition for the existence and uniqueness of the solution to (a1) (the Lax–Milgram lemma). In 1971, I. Babuška [a2] gave the following significant generalization of this lemma: Let
) is a sufficient condition for the existence and uniqueness of the solution to (a1) (the Lax–Milgram lemma). In 1971, I. Babuška [a2] gave the following significant generalization of this lemma: Let 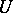 and
and 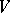 be two real Hilbert spaces and let
be two real Hilbert spaces and let 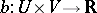 be a continuous bilinear functional. If it is also a weakly coercive (i.e., there exists a
be a continuous bilinear functional. If it is also a weakly coercive (i.e., there exists a 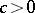 such that
such that
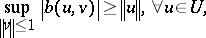 |
and
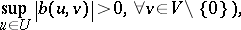 |
then for all 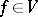 there exists a unique solution
there exists a unique solution 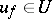 such that
such that 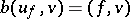 for all
for all 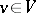 and, moreover,
and, moreover, 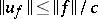 .
.
Sufficient and necessary conditions for a linear variational problem (a1) to have a unique solution depending continuously on the data 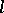 are given in [a3], namely: Let
are given in [a3], namely: Let 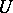 be a Banach space, let
be a Banach space, let 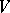 be a reflexive Banach space (cf. Reflexive space) and let
be a reflexive Banach space (cf. Reflexive space) and let 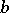 be a real functional on
be a real functional on 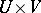 . The following statements are equivalent:
. The following statements are equivalent:
i) 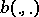 is a bilinear continuous weakly coercive functional;
is a bilinear continuous weakly coercive functional;
ii) there exists a linear, continuous and surjective operator 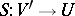 such that
such that 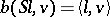 for all
for all 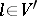 and
and 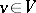 .
.
This result can be used to give simple examples of bilinear weakly coercive functionals that are not strongly coercive. Indeed, let 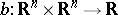 be the bilinear functional generated by a square non-singular matrix
be the bilinear functional generated by a square non-singular matrix 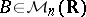 (i.e.,
(i.e.,  ). Then
). Then 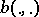 is weakly coercive, because for all
is weakly coercive, because for all 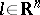 there exists a unique solution,
there exists a unique solution, 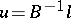 , for (a1); however, it is strongly coercive if and only if
, for (a1); however, it is strongly coercive if and only if 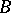 is either strictly positive (i.e.,
is either strictly positive (i.e., 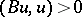 for all
for all 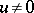 ) or strictly negative (i.e.,
) or strictly negative (i.e., 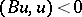 for all
for all 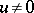 ).
).
Using this fact one can prove that if 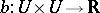 is symmetric (i.e.,
is symmetric (i.e., 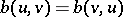 ) and strictly defined (i.e.,
) and strictly defined (i.e., 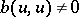 for all
for all 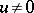 ), then it is either a strictly positive functional (i.e.,
), then it is either a strictly positive functional (i.e., 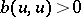 for all
for all 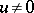 ) or a strictly negative functional (i.e.,
) or a strictly negative functional (i.e., 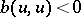 for all
for all 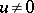 ); moreover
); moreover 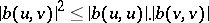 for all
for all 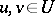 . The following result can also be found in [a3]: If
. The following result can also be found in [a3]: If 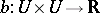 is a symmetric and continuous functional then it is strongly coercive if and only if it is weakly coercive and strictly defined. This implies that if
is a symmetric and continuous functional then it is strongly coercive if and only if it is weakly coercive and strictly defined. This implies that if 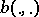 is a symmetric and strictly defined functional, then it is strongly coercive if and only if it is weakly coercive.
is a symmetric and strictly defined functional, then it is strongly coercive if and only if it is weakly coercive.
Effective applications of the Babuška–Lax–Millgram theorem can be found in [a4].
References
| [a1] | P.D. Lax, A.N. Milgram, "Parabolic equations" Ann. Math. Studies , 33 (1954) pp. 167–190 |
| [a2] | I. Babuška, "Error bound for the finite element method" Numer. Math. , 16 (1971) pp. 322–333 |
| [a3] | I. Roşca, "On the Babuška Lax Milgram theorem" An. Univ. Bucureşti , XXXVIII : 3 (1989) pp. 61–65 |
| [a4] | I. Babuška, A.K. Aziz, "Survey lectures on the mathematical foundations of finite element method" A.K. Aziz (ed.) , The Mathematical Foundations of the FEM with Application to PDE , Acad. Press (1972) pp. 5–359 |
Babuska-Lax-Milgram theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Babuska-Lax-Milgram_theorem&oldid=12089