Alexander invariants
Invariants connected with the module structure of the one-dimensional homology of a manifold 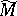 , freely acted upon by a free Abelian group
, freely acted upon by a free Abelian group  of rank
of rank  with a fixed system of generators
with a fixed system of generators 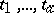 .
.
The projection of the manifold  onto the space
onto the space  of orbits (cf. Orbit) is a covering which corresponds to the kernel
of orbits (cf. Orbit) is a covering which corresponds to the kernel 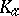 of the homomorphism
of the homomorphism 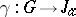 of the fundamental group
of the fundamental group 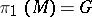 of the manifold
of the manifold  . Since
. Since 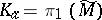 , the group
, the group  , where
, where 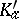 is the commutator subgroup of the kernel
is the commutator subgroup of the kernel 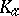 , is isomorphic to the one-dimensional homology group
, is isomorphic to the one-dimensional homology group 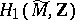 . The extension
. The extension 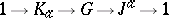 generates the extension
generates the extension 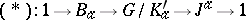 , which determines on
, which determines on  the structure of a module over the integer group ring
the structure of a module over the integer group ring 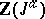 of the group
of the group  (cf. Group algebra). The same structure is induced on
(cf. Group algebra). The same structure is induced on  by the given action of
by the given action of  on
on 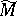 . Fixation of the generators
. Fixation of the generators 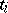 in
in 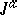 identifies
identifies  with the ring
with the ring 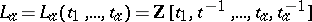 of Laurent polynomials in the variables
of Laurent polynomials in the variables  . Purely algebraically the extension
. Purely algebraically the extension
defines and is defined by the extension of modules 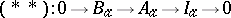 [5]. Here
[5]. Here  is the kernel of the homomorphism
is the kernel of the homomorphism 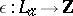
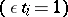 . The module
. The module 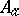 is called the Alexander module of the covering
is called the Alexander module of the covering  . In the case first studied by J.W. Alexander [1] when
. In the case first studied by J.W. Alexander [1] when 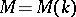 is the complementary space of some link
is the complementary space of some link 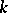 of multiplicity
of multiplicity 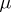 in the three-dimensional sphere
in the three-dimensional sphere  , while the covering corresponds to the commutation homomorphism
, while the covering corresponds to the commutation homomorphism 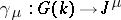 of the link group,
of the link group,  is the Alexander module of the link
is the Alexander module of the link  . The principal properties of
. The principal properties of  which are relevant to what follows are:
which are relevant to what follows are: 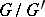 is a free Abelian group, the defect of the group
is a free Abelian group, the defect of the group  is 1,
is 1,  has the presentation
has the presentation 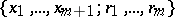 for which
for which 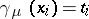 ,
, 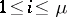 ;
; 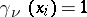 ,
, 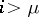 (cf. Knot and link diagrams). In the case of links the generators
(cf. Knot and link diagrams). In the case of links the generators 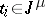 correspond to the meridians of the components
correspond to the meridians of the components  and are fixed by the orientations of these components and of the sphere.
and are fixed by the orientations of these components and of the sphere.
As a rule,  is the complementary space
is the complementary space  of
of 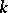 , consisting of
, consisting of 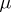
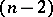 -dimensional spheres
-dimensional spheres 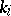 in
in 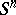 . In addition to the homomorphism
. In addition to the homomorphism 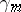 , one also considers the homomorphism
, one also considers the homomorphism 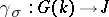 , where
, where 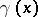 is equal to the sum of the link coefficients of the loop representing
is equal to the sum of the link coefficients of the loop representing  with all
with all 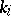 .
.
The matrix  of the module relations of a module
of the module relations of a module 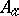 is called the Alexander covering matrix and, in the case of links, the Alexander link matrix. It may be obtained as the matrix
is called the Alexander covering matrix and, in the case of links, the Alexander link matrix. It may be obtained as the matrix
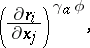 |
where 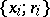 is a presentation of the group
is a presentation of the group 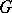 . If
. If 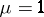 , the matrix
, the matrix 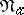 of module relations for
of module relations for  is obtained from
is obtained from 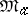 by discarding the zero column. The matrices
by discarding the zero column. The matrices  and
and 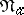 are defined by the modules
are defined by the modules 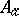 and
and 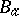 up to transformations corresponding to transitions to other presentations of the module. However, they can be used to calculate a number of module invariants. Alexander ideals are ideals of the module
up to transformations corresponding to transitions to other presentations of the module. However, they can be used to calculate a number of module invariants. Alexander ideals are ideals of the module 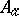 , i.e. series of ideals
, i.e. series of ideals 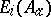 of the ring
of the ring 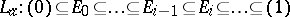 , where
, where 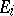 is generated by the minors of
is generated by the minors of  of order
of order 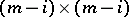 and
and 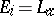 for
for 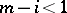 . The opposite numbering sequence may also be employed. Since
. The opposite numbering sequence may also be employed. Since 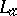 is both a Gaussian ring and a Noetherian ring, each ideal
is both a Gaussian ring and a Noetherian ring, each ideal 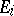 lies in a minimal principal ideal
lies in a minimal principal ideal 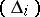 ; its generator
; its generator 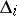 is defined up to unit divisors
is defined up to unit divisors 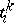 . The Laurent polynomial
. The Laurent polynomial 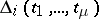 is simply called the Alexander polynomial of
is simply called the Alexander polynomial of 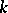 (or of the covering
(or of the covering  ). If
). If 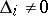 , it is multiplied by
, it is multiplied by 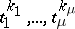 so that
so that 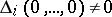 and
and 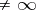 . To the homomorphism
. To the homomorphism 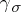 there correspond a module
there correspond a module  , ideals
, ideals 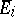 and polynomials
and polynomials 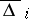 , designated, respectively, as Alexander's reduced module, Alexander's reduced ideals and Alexander's reduced polynomials of
, designated, respectively, as Alexander's reduced module, Alexander's reduced ideals and Alexander's reduced polynomials of  (or of the covering
(or of the covering  ). If
). If  , then
, then  .
. 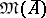 is obtained from
is obtained from 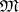 by replacing all
by replacing all 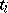 by
by 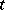 . If
. If 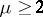 ,
, 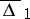 is divisible by
is divisible by 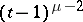 . The polynomial
. The polynomial 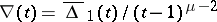 is known as the Hosokawa polynomial. The module properties of
is known as the Hosokawa polynomial. The module properties of  have been studied [4], [8], [10]. The case of links has not yet been thoroughly investigated. For
have been studied [4], [8], [10]. The case of links has not yet been thoroughly investigated. For  , the group
, the group 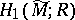 is finitely generated over any ring
is finitely generated over any ring 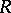 containing
containing 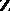 in which
in which 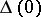 is invertible [7], in particular over the field of rational numbers, and, if
is invertible [7], in particular over the field of rational numbers, and, if  , then also over
, then also over  . In such a case
. In such a case  is the characteristic polynomial of the transformation
is the characteristic polynomial of the transformation 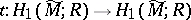 . The degree of
. The degree of 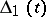 is equal to the rank of
is equal to the rank of 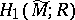 ; in particular,
; in particular, 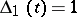 if and only if
if and only if 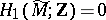 . If
. If 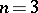 , the link ideals have the following symmetry property:
, the link ideals have the following symmetry property: 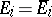 , where the bar denotes that the image is taken under the automorphism generated by replacing all
, where the bar denotes that the image is taken under the automorphism generated by replacing all  by
by 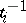 . It follows that
. It follows that 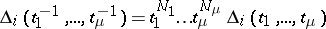 for certain integers
for certain integers 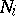 . This symmetry is the result of the Fox–Trotter duality for knot and link groups. It may also be deduced from the Poincaré duality for the manifold
. This symmetry is the result of the Fox–Trotter duality for knot and link groups. It may also be deduced from the Poincaré duality for the manifold 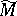 , taking into account the free action of
, taking into account the free action of  [3]. If
[3]. If  , then the chain complex
, then the chain complex 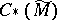 over the field of fractions
over the field of fractions 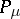 of the ring
of the ring  is acyclic (
is acyclic (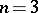 ), and the Reidemeister torsion
), and the Reidemeister torsion 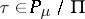 corresponding to the imbedding
corresponding to the imbedding 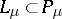 , where
, where 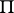 is the group of units of
is the group of units of  , is defined accordingly. If
, is defined accordingly. If 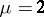 , then
, then  ; if
; if 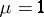 , then
, then 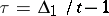 (up to units of
(up to units of 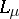 ). The symmetry of
). The symmetry of 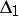 for
for 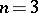 is a consequence of the symmetry of
is a consequence of the symmetry of  . If
. If 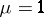 , it follows from the symmetry of
, it follows from the symmetry of  and from the property
and from the property 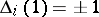 that the degree of
that the degree of 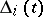 is even. The degree of
is even. The degree of 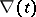 is also even [4]. The following properties of the knot polynomials
is also even [4]. The following properties of the knot polynomials  are characteristic:
are characteristic: 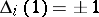 ;
; 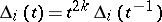 ;
; 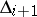 divides
divides 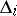 ; and
; and 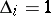 for all
for all 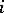 greater than a certain value
greater than a certain value 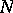 , i.e. for each selection
, i.e. for each selection  with these properties there exists a knot
with these properties there exists a knot  for which they serve as the Alexander polynomials. The Hosokawa polynomials [4] are characterized by the property
for which they serve as the Alexander polynomials. The Hosokawa polynomials [4] are characterized by the property 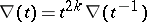 for any
for any 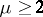 ; the polynomials
; the polynomials  of two-dimensional knots by the property
of two-dimensional knots by the property 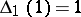 .
.
Alexander invariants, and in the first place the polynomials, are powerful tools for distinguishing knots and links. Thus, 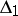 fails to distinguish between only three pairs out of the knots in a table containing fewer than 9 double points (cf. Knot table). See also Knot theory; Alternating knots and links.
fails to distinguish between only three pairs out of the knots in a table containing fewer than 9 double points (cf. Knot table). See also Knot theory; Alternating knots and links.
References
| [1] | J.W. Alexander, "Topological invariants of knots and links" Trans. Amer. Math. Soc. , 30 (1928) pp. 275–306 |
| [2] | K. Reidemeister, "Knotentheorie" , Chelsea, reprint (1948) |
| [3] | R.C. Blanchfield, "Intersection theory of manifolds with operators with applications to knot theory" Ann. of Math. (2) , 65 : 2 (1957) pp. 340–356 |
| [4] | F. Hosokawa, "On  -polynomials of links" Osaka J. Math. , 10 (1958) pp. 273–282 -polynomials of links" Osaka J. Math. , 10 (1958) pp. 273–282 |
| [5] | R.H. Crowell, "Corresponding groups and module sequences" Nagoya Math. J. , 19 (1961) pp. 27–40 |
| [6] | R.H. Crowell, R.H. Fox, "Introduction to knot theory" , Ginn (1963) |
| [7] | L.P. Neuwirth, "Knot groups" , Princeton Univ. Press (1965) |
| [8] | R.H. Crowell, "Torsion in link modules" J. Math. Mech. , 14 : 2 (1965) pp. 289–298 |
| [9] | J. Levine, "A method for generating link polynomials" Amer. J. Math. , 89 (1967) pp. 69–84 |
| [10] | J.W. Milnor, "Multidimensional knots" , Conference on the topology of manifolds , 13 , Boston (1968) pp. 115–133 |
Alexander invariants. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Alexander_invariants&oldid=12088