Cylinder set
A set  in a vector space
in a vector space  over the field
over the field  of real numbers given by an equation
of real numbers given by an equation
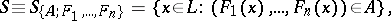 |
where  ,
,  are linear functions defined on
are linear functions defined on  and
and  is a Borel set in the
is a Borel set in the  -dimensional space
-dimensional space 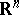 ,
,  .
.
The collection of all cylinder sets in  forms an algebra of sets, the so-called cylinder algebra. The smallest
forms an algebra of sets, the so-called cylinder algebra. The smallest  -algebra of subsets of
-algebra of subsets of  containing the cylinder sets is called the cylinder
containing the cylinder sets is called the cylinder  -algebra.
-algebra.
When  is a topological vector space, one considers only cylinder sets
is a topological vector space, one considers only cylinder sets  that are defined by collections
that are defined by collections 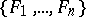 of continuous linear functions. Here by the cylinder algebra and the cylinder
of continuous linear functions. Here by the cylinder algebra and the cylinder  -algebra one understands the corresponding collection of subsets of
-algebra one understands the corresponding collection of subsets of  that are generated by precisely such cylinder sets. In the important special case when
that are generated by precisely such cylinder sets. In the important special case when  is the topological dual of some topological vector space
is the topological dual of some topological vector space 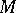 ,
, 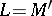 , cylinder sets in
, cylinder sets in  are defined by means of *-weakly continuous linear functions on
are defined by means of *-weakly continuous linear functions on  , that is, functions of the form
, that is, functions of the form
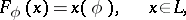 |
where  is an arbitrary element of
is an arbitrary element of  .
.
Comments
In a somewhat more general context, let  be a product of (topological) spaces. An
be a product of (topological) spaces. An  -cylinder set, or simply a cylinder set, in
-cylinder set, or simply a cylinder set, in  is a set of the form
is a set of the form 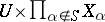 where
where 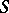 is a finite subset of
is a finite subset of 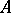 and
and  is a subset of
is a subset of 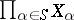 .
.
Cylinder set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cylinder_set&oldid=12082