Infinite decimal expansion
From Encyclopedia of Mathematics
A number written as a decimal fraction, such that there is no last digit. For example, 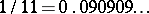 ,
, 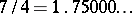 or
or 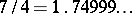 ,
, 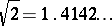 , etc. If the number is rational, the infinite decimal fraction is recurrent: starting from a certain digit, it consists of an infinitely recurring digit or group of digits called a period. In the above examples these are: 09 for
, etc. If the number is rational, the infinite decimal fraction is recurrent: starting from a certain digit, it consists of an infinitely recurring digit or group of digits called a period. In the above examples these are: 09 for 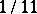 and 0 or 9 for
and 0 or 9 for 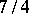 . If the number is irrational, the infinite decimal fraction cannot be recurrent (e.g.
. If the number is irrational, the infinite decimal fraction cannot be recurrent (e.g. 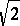 ).
).
Comments
The period length of the decimal expansion of a rational number 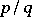 with
with 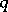 not divisible by 2 or 5, is precisely the smallest positive integer
not divisible by 2 or 5, is precisely the smallest positive integer  such that
such that 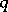 divides
divides  . Thus, the period length divides
. Thus, the period length divides  , the Euler function.
, the Euler function.
How to Cite This Entry:
Infinite decimal expansion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Infinite_decimal_expansion&oldid=12068
Infinite decimal expansion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Infinite_decimal_expansion&oldid=12068
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article