Schur theorems
Theorems for finding a solution to the coefficient problem for bounded analytic functions. They were obtained by I. Schur [1]. Let 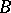 be the class of regular functions
be the class of regular functions  in
in 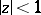 satisfying in it the condition
satisfying in it the condition 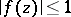 . Let
. Let 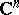 ,
, 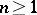 , be the
, be the  -dimensional complex Euclidean space, its points are
-dimensional complex Euclidean space, its points are  -tuples of complex numbers
-tuples of complex numbers  ; let
; let  be a set of points
be a set of points 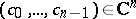 such that the numbers
such that the numbers  are the first
are the first  coefficients of some function from
coefficients of some function from 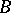 . The sets
. The sets  are closed, bounded and convex in
are closed, bounded and convex in 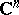 . Then the following theorems hold.
. Then the following theorems hold.
Schur's first theorem: To the points  on the boundary of
on the boundary of 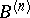 there correspond in
there correspond in 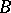 only rational functions of the form
only rational functions of the form
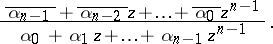 |
Schur's second theorem: A necessary and sufficient condition for 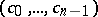 to be an interior point of
to be an interior point of  is that the following inequalities hold for
is that the following inequalities hold for 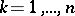 :
:
 |
Schur's second theorem provides the complete solution to the coefficient problem for bounded functions in the case of interior points of the coefficients region.
References
| [1] | I. Schur, "Ueber Potentzreihen, die im Innern des Einheitkreises berchränkt sind" J. Reine Angew. Math. , 147 (1917) pp. 205–232 |
| [2] | L. Bieberbach, "Lehrbuch der Funktionentheorie" , 2 , Teubner (1931) |
| [3] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
Comments
References
| [a1] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11 |
| [a2] | J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981) pp. 40 |
Schur theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schur_theorems&oldid=12059