Kernel of a matrix
From Encyclopedia of Mathematics
A matrix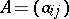 
of size 
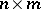over a field 
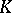defines a linear function 
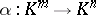between the standard vector spaces 
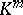and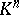 
by the well-known formula
 |
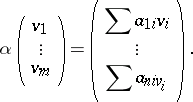The kernel of the matrix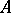 
is the kernel of the linear mapping 
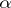. The kernel of 
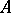(respectively, of 
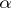) is also called the null space or nullspace of 
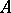(respectively, 
).
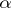References
| [a1] | G. Strang, "Linear algebra and its applications" , Harcourt–Brace–Jovanovich (1988) pp. 92 |
| [a2] | H. Schneider, G.P. Barker, "Matrices and linear algebra" , Dover, reprint (1989) pp. 215 |
| [a3] | B. Noble, J.W. Daniel, "Applied linear algebra" , Prentice-Hall (1977) pp. 157 |
| [a4] | Ch.G. Cullen, "Matrices and linear transformations" , Dover, reprint (1990) pp. 187 |
How to Cite This Entry:
Kernel of a matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kernel_of_a_matrix&oldid=12040
Kernel of a matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kernel_of_a_matrix&oldid=12040
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article