Superefficient estimator
hyperefficient estimator
An abbreviation of the phrase "superefficient sequence of estimators" , used for a consistent sequence of asymptotically-normal estimators of an unknown parameter that is better (more efficient) than a consistent sequence of maximum-likelihood estimators.
Let 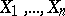 be independent identically-distributed random variables that take values in a sampling space
be independent identically-distributed random variables that take values in a sampling space  ,
, 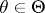 . Suppose that the family of distributions
. Suppose that the family of distributions 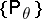 is such that there is a consistent sequence
is such that there is a consistent sequence 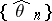 of maximum-likelihood estimators
of maximum-likelihood estimators 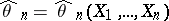 of the parameter
of the parameter 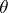 . Let
. Let 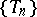 be a sequence of asymptotically-normal estimators
be a sequence of asymptotically-normal estimators 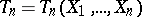 of
of  . If
. If
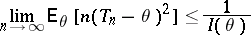 |
for all 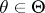 , where
, where  is the Fisher amount of information, and if, in addition, the strict inequality
is the Fisher amount of information, and if, in addition, the strict inequality
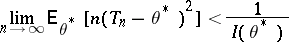 | (*) |
holds at least at one point  , then the sequence
, then the sequence 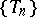 is called superefficient relative to the quadratic loss function, and the points
is called superefficient relative to the quadratic loss function, and the points 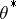 at which (*) holds are called points of superefficiency.
at which (*) holds are called points of superefficiency.
References
| [1] | I.A. Ibragimov, R.Z. [R.Z. Khas'minskii] Has'minskii, "Statistical estimation: asymptotic theory" , Springer (1981) (Translated from Russian) |
| [2] | L. Schmetterer, "Introduction to mathematical statistics" , Springer (1974) (Translated from German) |
| [3] | L. le Cam, "On some asymptotic properties of maximum likelihood estimates and related Bayes estimates" Univ. California Publ. Stat. , 1 (1953) pp. 277–330 |
Superefficient estimator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Superefficient_estimator&oldid=12034