Gibbs phenomenon

A characteristic of the behaviour of the partial sums (or their averages) of a Fourier series.

Figure: g044410a

First noted by H. Wilbraham [1] and rediscovered by J.W. Gibbs [2] at a much later date. Let the partial sums of the Fourier series of a function converge to in some neighbourhood of a point at which

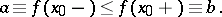The Gibbs phenomenon takes place for at if where

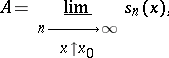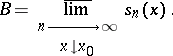The geometrical meaning of this is that the graphs (cf. Fig.) of the partial sums 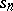do not approach the "expected" interval on the vertical line , but approach the strictly-larger interval as and . The Gibbs phenomenon is defined in an analogous manner for averages of the partial sums of a Fourier series when the latter is summed by some given method.

For instance, the following theorems are valid for 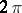-periodic functions of bounded variation on 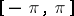[3].

1) At points of non-removable discontinuity, and only at such points, the Gibbs phenomenon occurs for . In particular, if for , then for the point the segment , while the segment 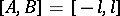where

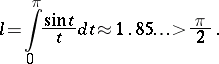2) There exists an absolute constant , , 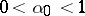such that the Cesàro averages do not have the Gibbs phenomenon if , while if the phenomenon is observed at all points of non-removable discontinuity of .

References

[1]	H. Wilbraham, Cambridge and Dublin Math. J. , 3 (1848) pp. 198–201
[2]	J.W. Gibbs, Nature , 59 (1898) pp. 200
[3]	A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988)

Comments

In a more explicit form the definitions of the constant and 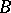above are:

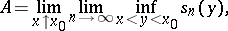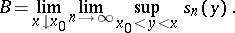At an isolated jump discontinuity of , the ratio equals 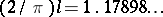. This means that the Fourier series approximation establishes an overshoot of about of the length of the jump at either end of the jump interval.

Actually, it was only in a second letter to ([a1]) that Gibbs stated the phenomenon correctly, though without any proof. For details see [a2].

References

[a1]	J.W. Gibbs, Nature , 59 (1899) pp. 606
[a2]	H.S. Carslaw, "Introduction to the theory of Fourier's series and integrals" , Dover, reprint (1930)