Affine unimodular group
equi-affine group
The subgroup of the general affine group consisting of the affine transformations of the  -dimensional affine space
-dimensional affine space
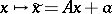 | (*) |
that satisfy the condition 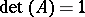 . If the vectors
. If the vectors  and
and 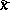 are interpreted as rectangular coordinates of points in the
are interpreted as rectangular coordinates of points in the  -dimensional Euclidean space
-dimensional Euclidean space 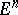 , then the transformation (*) will preserve the volumes of
, then the transformation (*) will preserve the volumes of  -dimensional domains of
-dimensional domains of 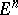 . This makes it possible to introduce the concept of volume in an equi-affine space, which is a space with a fundamental affine unimodular group. If, in formulas (*), one puts
. This makes it possible to introduce the concept of volume in an equi-affine space, which is a space with a fundamental affine unimodular group. If, in formulas (*), one puts 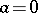 , then one obtains a centro-affine unimodular group of transformations isomorphic to the group of all matrices of order
, then one obtains a centro-affine unimodular group of transformations isomorphic to the group of all matrices of order  with determinant equal to one. Such a group of matrices is called the unimodular group or special linear group of order
with determinant equal to one. Such a group of matrices is called the unimodular group or special linear group of order  and is denoted by
and is denoted by 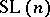 .
.
Affine unimodular group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Affine_unimodular_group&oldid=12002