Shirshov basis
Širšov basis
A particular basis for free Lie algebras introduced in [a1]. It is identical, up to symmetries, to the Lyndon basis (cf Lyndon word; Lie algebra, free).
A word is a sequence of letters 
, that is, elements chosen from a set 
called an alphabet. A word is usually written as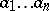 
, or abbreviated by a single symbol: 
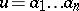. The length of 
is equal to the number of letters in 
, i.e. 
. One may concatenate words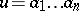 
, 
and this operation is concisely written as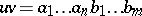 
. The set of all words over 
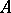is denoted by 
.
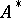Shirshov's original description, as given in [a2], is as follows. Let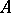 
be a set totally ordered by a relation 
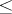(cf. Totally ordered set). Extend the order to all words by setting 
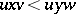and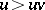 
for all 
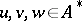and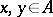 
such that 
.
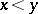Let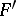 
be the set of words 
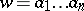strictly greater, with respect to 
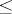, than any of their circular shifts 
(
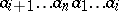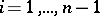). Shirshov's lemma [a1] shows that any word 
is a non-decreasing product of words in 
: 
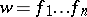with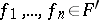 
and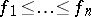 
. As for Lyndon words (cf. Lyndon word), words in 
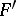lead to a basis of the free Lie algebra (over 
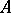; cf. Lie algebra, free). Indeed, only a bracketing 
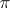of words in 
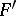is needed. This is done inductively as follows. Set 
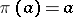for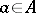 
. Otherwise, a 
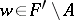may be written as 
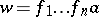with 
, 
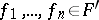and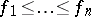 
. Then one defines
 |
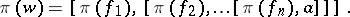The set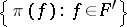 
is the Shirshov basis for the free Lie algebra over 
.
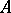References
| [a1] | A.I. Shirshov, "On bases for free Lie algebras" Algebra i Logika Sém. , 1 (1962) pp. 14–19 (In Russian) |
| [a2] | X. Viennot, "Algèbres de Lie libres et monoïdes libres" , Lecture Notes in Mathematics , 691 , Springer (1978) |
Shirshov basis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Shirshov_basis&oldid=11952