Hilbert singular integral
From Encyclopedia of Mathematics
The improper integral (in the sense of the Cauchy principal value)
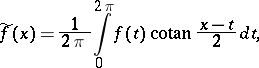 |
where the periodic function 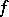 is called the density of the Hilbert singular integral, while
is called the density of the Hilbert singular integral, while 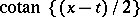 is called its kernel. If
is called its kernel. If 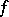 is summable,
is summable, 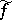 exists almost-everywhere; if
exists almost-everywhere; if 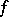 satisfies the Lipschitz condition of order
satisfies the Lipschitz condition of order 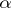 ,
, 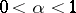 ,
, 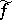 exists for any
exists for any  and satisfies this condition as well. If
and satisfies this condition as well. If 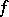 has summable
has summable 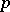 -th power,
-th power, 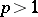 ,
, 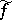 has the same property, and
has the same property, and
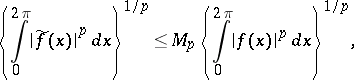 |
where 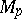 is a constant independent of
is a constant independent of 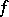 . In addition, the inversion formula of Hilbert's singular integral,
. In addition, the inversion formula of Hilbert's singular integral,
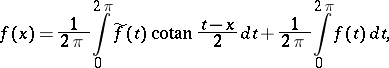 |
is valid. The function 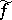 is said to be conjugate with
is said to be conjugate with 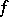 .
.
References
| [1] | D. Hilbert, "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen" , Chelsea, reprint (1953) |
| [2] | M. Riesz, "Sur les fonctions conjugées" Math. Z. , 27 (1927) pp. 218–244 |
| [3] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [4] | N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1972) (Translated from Russian) |
Comments
See also Hilbert kernel; Hilbert transform.
References
| [a1] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
| [a2] | B.L. Moiseiwitsch, "Integral equations" , Longman (1977) |
How to Cite This Entry:
Hilbert singular integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert_singular_integral&oldid=11933
Hilbert singular integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert_singular_integral&oldid=11933
This article was adapted from an original article by B.V. Khvedelidze (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article