Semi-pseudo-Euclidean space
A vector space with a degenerate indefinite metric. The semi-pseudo-Euclidean space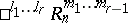 
is defined as an 
-dimensional space in which there are given 
scalar products
 |
where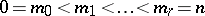 
; 
; 
; 
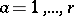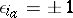, and 
occurs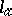 
times among the numbers 
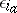. The product 
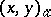is defined for those vectors for which all coordinates 
, 
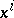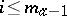or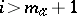 
, are zero. The first scalar square of an arbitrary vector 
of a semi-pseudo-Euclidean space is a degenerate quadratic form in the vector coordinates:
 |
where 
is the index and 
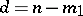is the defect of the space. If 
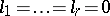, the semi-pseudo-Euclidean space is a semi-Euclidean space. Straight lines, 
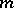-dimensional planes 
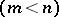, parallelism, and length of vectors, are defined in semi-pseudo-Euclidean spaces in the same way as in pseudo-Euclidean spaces. In the semi-pseudo-Euclidean space 
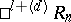one can choose an orthogonal basis consisting of 
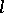vectors of imaginary length, of 
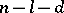of real length and of 
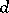isotropic vectors. Through every point of a semi-pseudo-Euclidean space of defect 
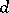passes an 
-dimensional isotropic plane all vectors of which are orthogonal to all vectors of the space. See also Galilean space.
References
| [1] | B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian) |
Comments
References
| [a1] | B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian) |
Semi-pseudo-Euclidean space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-pseudo-Euclidean_space&oldid=11931