Representation function

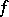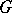A continuous function on a topological space endowed with a continuous action of a group , whose orbit 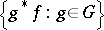in the space of all continuous functions on 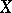generates a finite-dimensional subspace. Representation functions are also called spherical, or almost-invariant, functions. The representation functions with values in the field 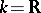or 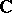form a -invariant 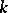-subalgebra 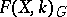in the algebra 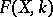of all 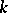-valued continuous functions on 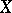. If 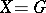is a topological group acting on itself by left shifts, 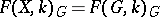coincides with the subspace in 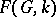generated by the matrix elements of finite-dimensional continuous linear representations o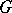f . If 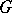is, moreover, a compact group, then one may restrict to matrix elements of irreducible representations. E.g., if 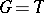is the rotation group of the plane, then the representation functions on 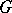are the trigonometric polynomials. Another example is furnished by the classical spherical functions on the sphere, which are representation functions for the standard action of the rotation group of the sphere.

If 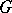is a compact topological group, continuously acting on a space 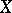that is a countable union of compacta, then 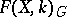is dense in 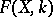in the compact-open topology (cf. Peter–Weyl theorem). Analogous statements hold for representation functions of various degrees of smoothness on a differentiable manifold with a smooth action of a compact Lie group. On the other hand, if 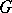does not allow for non-trivial continuous homomorphisms into a compact group (e.g. 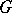is a connected semi-simple Lie group without compact simple factors), then every representation function on a compact space 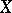with continuous action of 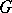is 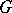-invariant [4].

If a smooth action of a compact Lie group 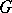on a differentiable manifold 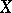has only a finite number of orbit types, then the algebra 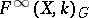of all representation functions of class 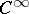is finitely generated over the subalgebra of all 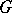-invariant functions of class 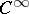(cf. [5]). In particular, for a homogeneous space 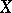the algebra 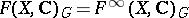is finitely generated and can be identified with the algebra of regular functions on the affine homogeneous algebraic variety over 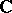whose set of real points coincides with 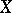. The problem of decomposing a 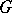-module 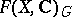into a direct sum of simple 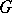-modules is important for applications. In case is the symmetric homogeneous space of a compact group 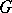it was solved by E. Cartan [1].

A generalization of representation functions are representation sections of a vector 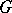-bundle 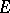over a 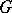-space 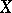, i.e. continuous sections whose 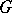-orbits generate a finite-dimensional subspace in the space 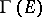of all continuous sections, e.g. representation tensor fields on smooth manifolds with a smooth action of a Lie group 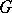; they form the 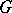-submodule 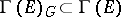(cf. [5]). If 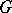is a compact group, the submodule 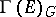is dense in 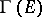. In case 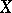is the symmetric homogeneous space of , the decomposition of the 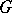-module 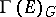into simple components has been studied (cf. [3]). If 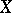is the compact homogeneous space of a semi-simple Lie group 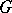without compact factors with a connected stationary subgroup, then

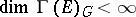(cf. [2]).

References

[1]	E. Cartan, "Sur la détermination d'un système orthogonal complet dans un espace de Riemann symmétrique clos" Rend. Circ. Mat. Palermo , 53 (1929) pp. 217–252
[2]	Van Cha Dao, "Spherical sections on a compact homogeneous space" Uspekhi Mat. Nauk , 30 : 5 (1975) pp. 203–204 (In Russian)
[3]	Yu.V. Dzyadyk, "On the determination of the spectrum of an induced representation on a compact symmetric space" Soviet Math. Dokl. , 16 (1975) pp. 193–197 Dokl. Akad. Nauk SSSR , 220 : 5 (1975) pp. 1019–1022
[4]	A.M. Lukatskii, Uspekhi Mat. Nauk , 26 : 5 (1971) pp. 212–213
[5]	A.L. Onishchik, "On invariants and almost invariants of compact transformation groups" Trans. Moscow Math. Soc. , 35 (1976) pp. 237–267 Trudy Moskov. Mat. Obshch. , 35 (1976) pp. 235–264

Comments

A more common name for "representation function" is 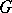-finite function. The term "spherical function" usually has another meaning, see (the editorial comments to) Spherical functions. For Cartan's work [1] on the decomposition of 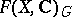in the case of a compact symmetric space 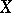see [a1], Chapt. V.

References

[a1]	S. Helgason, "Groups and geometric analysis" , Acad. Press (1984) pp. Chapt. II, Sect. 4