Continuous functional
A continuous operator (continuous mapping) mapping a topological space  , which as a rule is also a vector space, into
, which as a rule is also a vector space, into 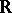 or
or 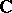 . Therefore, the definition of, and criteria for, continuity of an arbitrary operator continue to hold for functionals. For example,
. Therefore, the definition of, and criteria for, continuity of an arbitrary operator continue to hold for functionals. For example,
1) for a functional 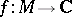 , where
, where  is a subset of a topological space
is a subset of a topological space 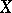 , to be continuous at a point
, to be continuous at a point 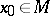 there must for any
there must for any 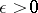 be a neighbourhood
be a neighbourhood 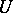 of
of 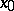 such that
such that 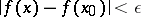 for
for 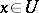 (definition of continuity of functionals);
(definition of continuity of functionals);
2) a functional that is continuous on a compact set of a separable topological vector space is bounded on this set and attains its least upper and greatest lower bounds (Weierstrass' theorem);
3) since every non-zero linear functional maps a Banach space 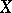 onto the whole of
onto the whole of 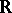 (or
(or 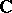 ), it induces an open mapping, that is, the image of any open set
), it induces an open mapping, that is, the image of any open set 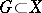 is an open set in
is an open set in 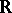 (or
(or  ).
).
Comments
References
| [a1] | A.E. Taylor, D.C. Lay, "Introduction to functional analysis" , Wiley (1980) |
Continuous functional. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_functional&oldid=11921