Lemniscates
Plane algebraic curves of order 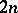 such that the product of the distances of each point of the curve from
such that the product of the distances of each point of the curve from  given points (foci)
given points (foci) 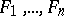 is equal to the
is equal to the  -th power of a given number
-th power of a given number  (the radius of the lemniscate). The equation of a lemniscate in rectangular Cartesian coordinates is
(the radius of the lemniscate). The equation of a lemniscate in rectangular Cartesian coordinates is
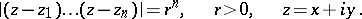 |
A circle is a lemniscate with one focus, and a Cassini oval is a lemniscate with two foci. See also Bernoulli lemniscate and Booth lemniscate.
Comments
References
| [a1] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
A lemniscate is a level curve of a polynomial. If all the foci 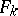 :
: 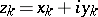 ,
, 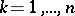 , are distinct and the radius of the lemniscate is sufficiently small, then the lemniscate consists of
, are distinct and the radius of the lemniscate is sufficiently small, then the lemniscate consists of  continua that have pairwise no common points. For a sufficiently large radius a lemniscate consists of one connected component. As D. Hilbert showed in 1897, the boundary
continua that have pairwise no common points. For a sufficiently large radius a lemniscate consists of one connected component. As D. Hilbert showed in 1897, the boundary 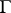 of an arbitrary simply-connected finite domain can be arbitrarily closely approximated by a lemniscate, that is, for any
of an arbitrary simply-connected finite domain can be arbitrarily closely approximated by a lemniscate, that is, for any 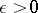 one can find a lemniscate
one can find a lemniscate 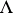 such that in the
such that in the  -neighbourhood of each point of
-neighbourhood of each point of 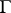 there are points of
there are points of 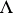 and every point of
and every point of 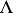 is in the
is in the  -neighbourhood of an appropriate point of
-neighbourhood of an appropriate point of 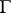 .
.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [2] | J.L. Walsh, "Interpolation and approximation by rational functions in the complex domain" , Amer. Math. Soc. (1965) |
E.D. Solomentsev
Lemniscates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lemniscates&oldid=11912