Spectrum of a dynamical system

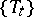with phase space 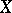and invariant measure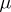

A common name for various spectral invariants and spectral properties of the corresponding group (or semi-group) of unitary (isometric) shift operators:

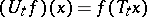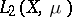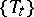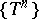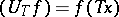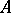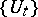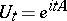in the Hilbert space . For a dynamical system in the narrow sense (a measurable flow or a cascade ), the spectral invariants of just one normal operator are meant: in the second case of the unitary operator , and in the first, of the generating self-adjoint operator that is the infinitesimal generator of the one-parameter group of unitary operators (here , by Stone's theorem).

The "spectral" terminology in the theory of dynamical systems differs somewhat from the ordinary usage. For all 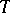and 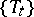of practical interest, the spectrum of 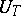(or 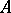) in the usual sense, that is, the set of those 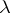for which the operat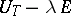or (or 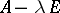) does not have a bounded inverse (cf. Spectrum of an operator), coincides with the circle 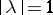or with 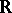(see [1], [2]). Therefore: a) the spectrum in the usual sense does not contain information about the properties of a given dynamical system which distinguish it from others; b) in the spectrum in the normal sense of the word, there are hardly ever any isolated points, so that it is continuous (in the ordinary sense) and this again does not contain information about specific properties of a given system. For this reason, in the theory of dynamical systems one speaks of a continuous spectrum wheneve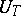r or 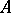have no eigenfunctions other than constants, of a discrete spectrum when the eigenfunctions form a complete system in 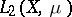and of a mixed spectrum in all other cases.

The properties of a dynamical system that are determined by its spectrum are called spectral properties. Examples are ergodicity (which is equivalent with the eigenvalue 1 of 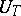, respectively of , being simple) and mixing. There is a complete metric classification of ergodic dynamical systems with a discrete spectrum: such a system is determined by its spectrum up to a metric isomorphism [3]. 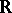An analogous theory has also been developed for transformation groups more general than and 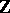(see [4]). In the non-commutative case formulations becomes more complicated, and, moreover, the spectrum no longer completely determines the system. If the spectrum is not discrete, then the situation is much more complex.

References

[1]	A. Ionescu Tulcea, "Random series and spectra of measure-preserving transformations" , Ergodic Theory (Tulane Univ. 1961) , Acad. Press (1963) pp. 273–292
[2]	S. Goldstein, "Spectrum of measurable flows" Astérisque , 40 (Internat. Conf. Dynam. Systems in Math. Physics) (1976) pp. 5–10
[3]	I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian)
[4]	G.W. Mackey, "Ergodic transformation groups with a pure point spectrum" Illinois J. Math. , 8 (1964) pp. 593–600

Comments

Instead of "discrete spectrum" also the term "pure point spectrum of a dynamical systempure point spectrum" is used in the literature. For transformation groups more general than 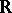and 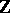and not necessarily commutative, also consult [a1] and [a2].

The next to simplest dynamical systems are those with a generalized discrete spectrum and those with a quasi-discrete spectrum. See [a4], [a3].

References

[a1]	R. Zimmer, "Extensions of ergodic group actions" Illinois J. Math. , 20 (1976) pp. 373–409
[a2]	R. Zimmer, "Ergodic actions with generalized discrete spectrum" Illinois J. Math , 20 (1976) pp. 555–588
[a3]	L.M. Abramov, "Metric automorphisms with quasi-discrete spectrum" Transl. Amer. Math. Soc. , 39 (1964) pp. 37–56 Izv. Akad. Nauk. SSSR Ser. Mat. , 26 (1962) pp. 513–530
[a4]	W. Parry, "Compact abelian group extensions of discrete dynamical systems" Z. Wahrsch. verw. Geb. , 13 (1969) pp. 95–113