Mercer theorem

The bilinear series

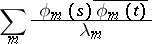of a Hermitian positive-definite continuous kernel 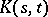on 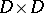(cf. Integral equation with symmetric kernel; Kernel of an integral operator), where 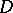is the closure of a bounded domain in 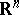, converges absolutely and uniformly in 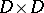to 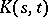. Here the 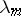are the characteristic numbers of the kernel 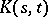and the 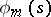are the corresponding orthonormalized eigen functions. If a kernel 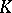satisfies the conditions of Mercer's theorem, then the integral operator ,

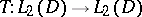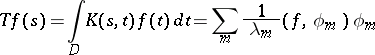is nuclear (cf. Nuclear operator) and its trace 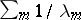can be calculated by the formula

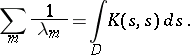Mercer's theorem can be generalized to the case of a bounded discontinuous kernel.

The theorem was proved by J. Mercer [1].

References

[1]	J. Mercer, Philos. Trans. Roy. Soc. London Ser. A , 209 (1909) pp. 415–446
[2]	J. Mercer, "Functions of positive and negative type, and their connection with the theory of integral equations" Proc. Roy. Soc. London Ser. A , 83 (1908) pp. 69–70
[3]	I.G. Petrovskii, "Lectures on the theory of integral equations" , Graylock (1957) (Translated from Russian)
[4]	F.G. Tricomi, "Integral equations" , Interscience (1957)
[5]	M.A. Krasnosel'skii, et al., "Integral operators in spaces of summable functions" , Noordhoff (1976) (Translated from Russian)

References

[a1]	I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1977)
[a2]	A.C. Zaanen, "Linear analysis" , North-Holland (1956)