Selberg sieve

Selberg method

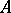A special, and at the same time fairly universal, sieve method created by A. Selberg [1]. The Selberg sieve enables one to obtain a good upper bound of the shifting function , which denotes the number of elements of a set of integers that are not divisible by prime numbers 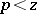and that belong to a certain set 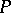of prime numbers.

Let 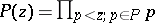. The Selberg method is based on the obvious inequality

(*)

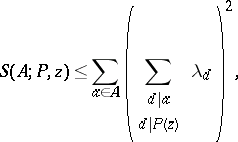which holds when 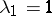for arbitrary real numbers 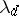(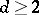). Selberg's idea consists of the following: Set 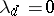for 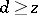, and minimize the right-hand side of (*) by a suitable choice of the remaining numbers ().

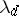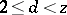When combined with other sieve methods, the Selberg sieve enables one to obtain lower bounds that are particularly powerful when used with weight functions.

References

[1]	A. Selberg, "On an elementary method in the theory of primes" Norsk. Vid. Selsk. Forh. , 19 : 18 (1947) pp. 64–67
[2]	K. Prachar, "Primzahlverteilung" , Springer (1957)
[3]	H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974)