Tate algebra
Let  be a field which is complete with respect to an ultrametric valuation
be a field which is complete with respect to an ultrametric valuation  (i.e.
(i.e.  ). The valuation ring
). The valuation ring 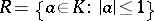 has a unique maximal ideal,
has a unique maximal ideal,  . The field
. The field 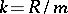 is called the residue field of
is called the residue field of 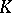 .
.
Examples of such fields are the local fields, i.e. finite extensions of the  -adic number field
-adic number field 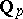 , or the field of Laurent series
, or the field of Laurent series 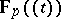 in
in 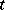 with coefficients in the finite field
with coefficients in the finite field 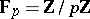 (cf. also Local field).
(cf. also Local field).
Let  denote indeterminates. Then
denote indeterminates. Then 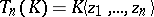 denotes the algebra of all power series
denotes the algebra of all power series  with
with  (
(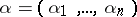 ) such that
) such that 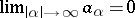 (
(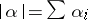 ). The norm on
). The norm on 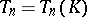 is given by
is given by 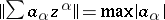 . The ring
. The ring  is denoted by
is denoted by 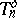 , and
, and 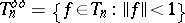 is an ideal of
is an ideal of  . Then
. Then 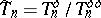 is easily seen to be the ring of polynomials
is easily seen to be the ring of polynomials 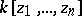 .
.
The 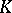 -algebra
-algebra 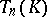 is called the free Tate algebra. An affinoid algebra, or Tate algebra,
is called the free Tate algebra. An affinoid algebra, or Tate algebra, 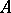 over
over 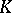 is a finite extension of some
is a finite extension of some 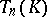 (i.e. there is a homomorphism of
(i.e. there is a homomorphism of 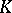 -algebras
-algebras 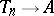 which makes
which makes 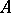 into a finitely-generated
into a finitely-generated 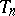 -module). The space of all maximal ideals,
-module). The space of all maximal ideals, 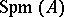 of a Tate algebra
of a Tate algebra 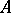 is called an affinoid space.
is called an affinoid space.
A rigid analytic space over 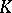 is obtained by glueing affinoid spaces. Every algebraic variety over
is obtained by glueing affinoid spaces. Every algebraic variety over  has a unique structure as a rigid analytic space. Rigid analytic spaces and affinoid algebras were introduced by J. Tate in order to study degenerations of curves and Abelian varieties over
has a unique structure as a rigid analytic space. Rigid analytic spaces and affinoid algebras were introduced by J. Tate in order to study degenerations of curves and Abelian varieties over 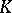 .
.
The theory of formal schemes over 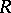 (the valuation ring of
(the valuation ring of 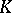 ) is close to that of rigid analytic spaces. This can be seen as follows.
) is close to that of rigid analytic spaces. This can be seen as follows.
Fix an element 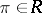 with
with 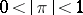 . The completion of
. The completion of 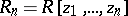 with respect to the topology given by the ideals
with respect to the topology given by the ideals  is the ring of strict power series
is the ring of strict power series 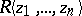 over
over  . Now
. Now 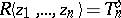 , and
, and 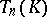 is the localization of
is the localization of  with respect to
with respect to 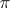 . So one can view
. So one can view 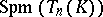 as the "general fibre" of the formal scheme
as the "general fibre" of the formal scheme  over
over 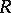 . More generally, any formal scheme
. More generally, any formal scheme 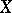 over
over 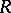 gives rise to a rigid analytic space over
gives rise to a rigid analytic space over 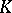 , the "general fibre" of
, the "general fibre" of 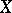 . Non-isomorphic formal schemes over
. Non-isomorphic formal schemes over 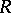 can have the same associated rigid analytic space over
can have the same associated rigid analytic space over 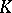 . Further, any reasonable rigid analytic space over
. Further, any reasonable rigid analytic space over 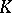 is associated to some formal scheme over
is associated to some formal scheme over 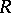 .
.
Affinoid spaces and affinoid algebras have many properties in common with affine spaces and affine rings over 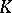 . Some of the most important are: Weierstrass preparation and division holds for
. Some of the most important are: Weierstrass preparation and division holds for 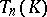 (cf. also Weierstrass theorem); affinoid algebras are Noetherian rings, and even excellent rings if the field
(cf. also Weierstrass theorem); affinoid algebras are Noetherian rings, and even excellent rings if the field 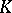 is perfect; for any maximal ideal
is perfect; for any maximal ideal  of an affinoid algebra
of an affinoid algebra 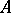 the quotient field
the quotient field  is a finite extension of
is a finite extension of 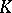 ; many finiteness theorems; any coherent sheaf
; many finiteness theorems; any coherent sheaf 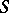 on an affinoid space
on an affinoid space 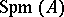 is associated to a finitely-generated
is associated to a finitely-generated 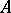 -module
-module  (further:
(further: 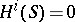 for
for 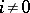 ).
).
Another interpretation of 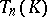 is:
is: 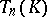 consists of all "holomorphic functions" on the polydisc
consists of all "holomorphic functions" on the polydisc  . This interpretation is useful for finding the holomorphic functions on more complicated spaces like Drinfel'd's symmetric spaces
. This interpretation is useful for finding the holomorphic functions on more complicated spaces like Drinfel'd's symmetric spaces 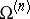 . Let
. Let 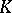 be a local field with algebraic closure
be a local field with algebraic closure 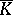 . Then
. Then
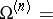 |
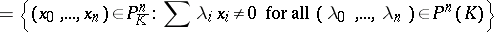 |
is a Drinfel'd symmetric space.
Spaces of this type have been used for the construction of Tate's elliptic curves, Mumford curves and surfaces, Shimura curves and varieties, etc.
References
| [a1] | S. Bosch, U. Güntzer, R. Remmert, "Non-Archimedean analysis" , Springer (1984) |
| [a2] | V.G. Drinfel'd, "Coverings of 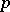 -adic symmetric regions" Funct. Anal. Appl. , 10 : 2 (1976) pp. 107–115 Funkts. Anal. Prilozhen. , 10 : 2 pp. 29–41 -adic symmetric regions" Funct. Anal. Appl. , 10 : 2 (1976) pp. 107–115 Funkts. Anal. Prilozhen. , 10 : 2 pp. 29–41 |
| [a3] | G. Faltings, "Arithmetische Kompaktifizierung des Modulraums der abelschen Varietäten" , Lect. notes in math. , 1111 , Springer (1984) |
| [a4] | J. Fresnel, M. van der Put, "Géométrie analytique rigide et applications" , Birkhäuser (1981) |
| [a5] | L. Gerritzen, M. van der Put, "Schottky groups and Mumford curves" , Lect. notes in math. , 817 , Springer (1980) |
| [a6] | D. Mumford, "An analytic construction of degenerating curves over complete local fields" Compos. Math. , 24 (1972) pp. 129–174 |
| [a7] | D. Mumford, "An analytic construction of degenerating abelian varieties over complete rings" Compos. Math. , 24 (1972) pp. 239–272 |
| [a8] | D. Mumford, "An algebraic surface with 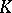 ample, ample, 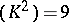 , , 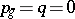 " Amer. J. Math. , 101 (1979) pp. 233–244 " Amer. J. Math. , 101 (1979) pp. 233–244 |
| [a9] | M. Raynaud, "Variétés abéliennes en géométrie rigide" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 2 , Gauthier-Villars (1971) pp. 473–477 |
| [a10] | J. Tate, "Rigid analytic spaces" Invent. Math. , 12 (1971) pp. 257–289 |
Tate algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tate_algebra&oldid=11874