Casimir element
Casimir operator
A central element of special form in the universal enveloping algebra of a semi-simple Lie algebra. Such operators were first introduced, for a particular case, by H. Casimir [1].
Let  be a semi-simple finite-dimensional Lie algebra over a field of characteristic
be a semi-simple finite-dimensional Lie algebra over a field of characteristic  , and let
, and let 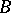 be an invariant symmetric bilinear form on
be an invariant symmetric bilinear form on 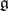 (that is,
(that is,  for all
for all 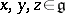 ) which is non-degenerate on a Cartan subalgebra
) which is non-degenerate on a Cartan subalgebra 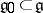 . Then a Casimir element of the Lie algebra
. Then a Casimir element of the Lie algebra  with respect to the form
with respect to the form 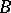 is an element of the universal enveloping algebra
is an element of the universal enveloping algebra 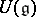 that is representable in the form
that is representable in the form
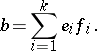 |
Here 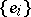 ,
, 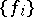 are dual bases of
are dual bases of 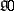 with respect to
with respect to 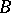 , that is,
, that is, 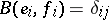 ,
, 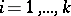 , where
, where 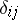 is the Kronecker symbol and
is the Kronecker symbol and  . The element
. The element 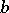 does not depend on the choice of the dual bases in
does not depend on the choice of the dual bases in 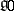 and belongs to the centre of
and belongs to the centre of 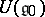 . If
. If  is a simple algebra, then a Casimir element of
is a simple algebra, then a Casimir element of 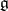 defined by the Killing form
defined by the Killing form 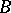 is the unique (up to a scalar multiplier) central element in
is the unique (up to a scalar multiplier) central element in 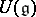 that is representable as a homogeneous quadratic polynomial in the elements of
that is representable as a homogeneous quadratic polynomial in the elements of 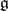 .
.
Every linear representation 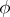 of a semi-simple algebra
of a semi-simple algebra 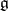 in a finite-dimensional space
in a finite-dimensional space 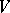 defines an invariant symmetric bilinear form
defines an invariant symmetric bilinear form
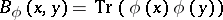 |
on 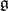 , which is non-degenerate on the subalgebra
, which is non-degenerate on the subalgebra 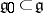 complementary to
complementary to 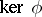 , and therefore also defines some Casimir element
, and therefore also defines some Casimir element 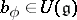 . If
. If  is an irreducible representation, then the extension of
is an irreducible representation, then the extension of 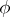 onto
onto 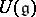 takes
takes  into
into 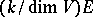 .
.
References
| [1] | H. Casimir, B.L. van der Waerden, "Algebraischer Beweis der Vollständigen Reduzibilität der Darstellungen halbeinfacher Liescher Gruppen" Math. Ann. , 111 (1935) pp. 1–2 |
| [2] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [3] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
| [4] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [5] | M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) |
| [6] | J. Dixmier, "Enveloping algebras" , North-Holland (1977) (Translated from French) |
Comments
The Casimir element 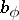 determined by
determined by 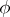 is called the Casimir element of the linear representation
is called the Casimir element of the linear representation 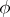 .
.
An additional good reference is [a1].
References
| [a1] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) |
Casimir element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Casimir_element&oldid=11861