Poisson process
A stochastic process  with independent increments
with independent increments 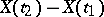 ,
,  , having a Poisson distribution. In the homogeneous Poisson process
, having a Poisson distribution. In the homogeneous Poisson process
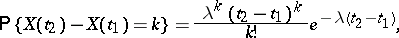 | (1) |
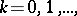 |
for any  . The coefficient
. The coefficient  is called the intensity of the Poisson process
is called the intensity of the Poisson process  . The trajectories of the Poisson process
. The trajectories of the Poisson process  are step-functions with jumps of height 1. The jump points
are step-functions with jumps of height 1. The jump points  form an elementary flow describing the demand flow in many queueing systems. The distributions of the random variables
form an elementary flow describing the demand flow in many queueing systems. The distributions of the random variables 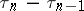 are independent for
are independent for 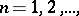 and have exponential density
and have exponential density 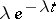 ,
,  .
.
One of the properties of a Poisson process is that the conditional distribution of the jump points  when
when  is the same as the distribution of the variational series of
is the same as the distribution of the variational series of  independent samples with uniform distribution on
independent samples with uniform distribution on  . On the other hand, if
. On the other hand, if  is the variational series described above, then as
is the variational series described above, then as  ,
,  and
and 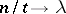 one obtains in the limit the distribution of the jumps of the Poisson process.
one obtains in the limit the distribution of the jumps of the Poisson process.
In an inhomogeneous process the intensity  depends on the time
depends on the time 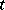 and the distribution of
and the distribution of  is defined by the formula
is defined by the formula
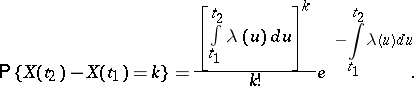 |
Under certain conditions a Poisson process can be shown to be the limit of the sum of a number of independent "sparse" flows of fairly general form as this number increases to infinity. For certain paradoxes which have been obtained in connection with Poisson processes see [3].
References
| [1] | A.A. Borovkov, "Wahrscheinlichkeitstheorie" , Birkhäuser (1976) (Translated from Russian) |
| [2] | I.I. Gikhman, A.V. Skorokhod, M.I. Yadrenko, "Probability theory and mathematical statistics" , Kiev (1979) (In Russian) |
| [3] | W. Feller, "An introduction to probability theory and its applications" , 2 , Wiley (1971) pp. Chapt. 1 |
Comments
References
| [a1] | J.W. Cohen, "The single server queue" , North-Holland (1982) |
| [a2] | G.G. Székely, "Paradoxes in probability theory and mathematical statistics" , Reidel (1986) |
Poisson process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poisson_process&oldid=11854