Parseval equality
An equality expressing the square of the norm of an element in a vector space with a scalar product in terms of the square of the moduli of the Fourier coefficients of this element in some orthogonal system. Thus, if 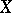 is a normed separable vector space with a scalar product
is a normed separable vector space with a scalar product 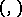 , if
, if  is the corresponding norm and if
is the corresponding norm and if 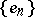 is an orthogonal system in
is an orthogonal system in 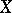 ,
, 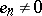 ,
, 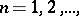 then Parseval's equality for an element
then Parseval's equality for an element 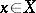 is
is
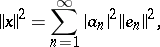 | (1) |
where 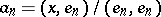 ,
, 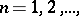 are the Fourier coefficients of
are the Fourier coefficients of  in the system
in the system 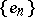 . If
. If 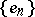 is orthonormal, then Parseval's equality has the form
is orthonormal, then Parseval's equality has the form
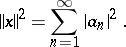 |
The validity of Parseval's equality for a given element 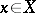 is a necessary and sufficient condition for its Fourier series in the orthogonal system
is a necessary and sufficient condition for its Fourier series in the orthogonal system 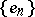 to converge to
to converge to  in the norm of
in the norm of 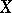 . The validity of Parseval's equality for every element
. The validity of Parseval's equality for every element 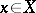 is a necessary and sufficient condition for the orthogonal system
is a necessary and sufficient condition for the orthogonal system 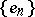 to be complete in
to be complete in 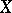 (cf. Complete system). This implies, in particular, that:
(cf. Complete system). This implies, in particular, that:
1) if 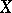 is a separable Hilbert space (cf. Hilbert space) and
is a separable Hilbert space (cf. Hilbert space) and 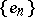 is an orthogonal basis of it, then Parseval's equality holds for
is an orthogonal basis of it, then Parseval's equality holds for 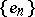 for every
for every 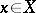 ;
;
2) if 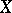 is a separable Hilbert space,
is a separable Hilbert space, 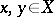 , if
, if 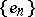 is an orthonormal basis of
is an orthonormal basis of 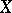 and if
and if 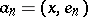 and
and 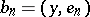 are the Fourier coefficients of
are the Fourier coefficients of  and
and 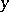 , then
, then
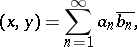 | (2) |
the so-called generalized Parseval equality. In a fairly-definitive form the question of the completeness of a system of functions that are the eigen functions of differential operators was studied by V.A. Steklov in [1].
Parseval's equality can also be generalized to the case of non-separable Hilbert spaces: If 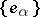 ,
, 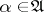 (
(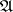 is a certain index set), is a complete orthonormal system in a Hilbert space
is a certain index set), is a complete orthonormal system in a Hilbert space 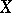 , then for any element
, then for any element 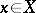 Parseval's equality holds:
Parseval's equality holds:
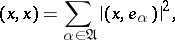 |
and the sum on the right-hand side is to be understood as
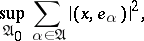 |
where the supremum is taken over all finite subsets 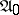 of
of 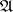 .
.
When 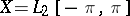 , the space of real-valued functions with Lebesgue-integrable squares on
, the space of real-valued functions with Lebesgue-integrable squares on 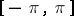 , and
, and 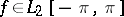 , then one may take the trigonometric system as a complete orthogonal system and
, then one may take the trigonometric system as a complete orthogonal system and
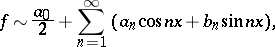 |
where (1) takes the form
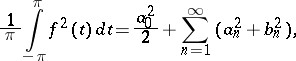 |
which is called the classical Parseval equality. It was proved in 1805 by M. Parseval.
If 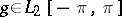 and
and
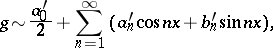 |
then an equality similar to (2) looks as follows:
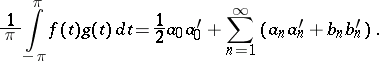 | (3) |
Two classes 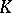 and
and 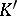 of real-valued functions defined on
of real-valued functions defined on 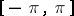 and such that for all
and such that for all 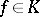 and
and 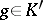 Parseval's equality (3) holds are called complementary. An example of complementary classes are the spaces
Parseval's equality (3) holds are called complementary. An example of complementary classes are the spaces 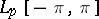 and
and 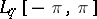 ,
,  ,
, 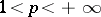 .
.
References
| [1] | V.A. Steklov, "Sur certaines égalités générales communes à plusieurs séries de fonctions souvent employées dans l'analyse" Zap. Nauchn. Fiz.-Mat. Obshch. Ser. 8 , 157 (1904) pp. 1–32 |
| [2] | S.M. Nikol'skii, "A course of mathematical analysis" , 2 , MIR (1977) (Translated from Russian) |
| [3] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 2 , MIR (1982) (Translated from Russian) |
| [4] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [5] | A. Zygmund, "Trigonometric series" , 1 , Cambridge Univ. Press (1988) |
| [6] | A.A. Kirillov, A.D. Gvishiani, "Theorems and problems in functional analysis" , Springer (1982) (Translated from Russian) |
Comments
References
| [a1] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
Parseval equality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parseval_equality&oldid=11840