Incomplete gamma-function
From Encyclopedia of Mathematics
The function defined by the formula
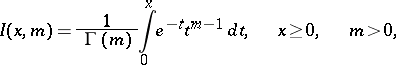 |
where 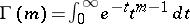 is the gamma-function. If
is the gamma-function. If 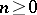 is an integer, then
is an integer, then
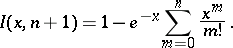 |
Series representation:
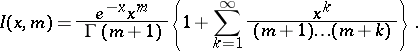 |
Continued fraction representation:
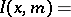 |
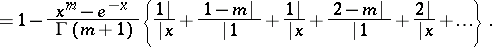 |
Asymptotic representation for large  :
:
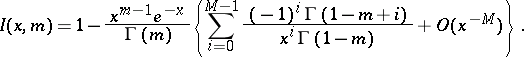 |
Asymptotic representation for large 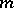 :
:
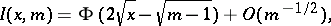 |
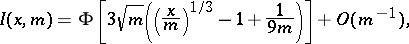 |
where
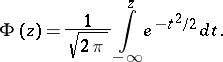 |
Connection with the confluent hypergeometric function:
 |
Connection with the Laguerre polynomials 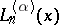 :
:
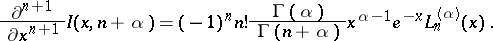 |
Recurrence relation:
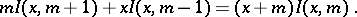 |
References
| [1] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1973) |
| [2] | V.I. Pagurova, "Tables of the incomplete gamma-function" , Moscow (1963) (In Russian) |
Comments
The following notations are also used:
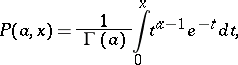 |
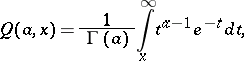 |
with 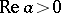 ,
, 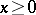 . The
. The 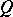 -function is related to the confluent hypergeometric function:
-function is related to the confluent hypergeometric function:
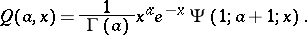 |
New asymptotic expansions for both 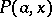 and
and 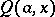 are given in [a1].
are given in [a1].
References
| [a1] | N.M. Temme, "The asymptotic expansion of the incomplete gamma functions" SIAM J. Math. Anal. , 10 (1979) pp. 757–766 |
How to Cite This Entry:
Incomplete gamma-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Incomplete_gamma-function&oldid=11834
Incomplete gamma-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Incomplete_gamma-function&oldid=11834
This article was adapted from an original article by V.I. Pagurova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article