Loop, analytic
An analytic manifold  endowed with the structure of a loop whose basic operations (multiplication, left and right division) are analytic mappings of
endowed with the structure of a loop whose basic operations (multiplication, left and right division) are analytic mappings of 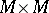 into
into 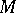 . If
. If  is the identity of the loop
is the identity of the loop 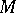 , and
, and 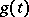 and
and 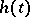 are analytic paths starting from
are analytic paths starting from  and having tangent vectors
and having tangent vectors  and
and 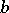 at
at  , then the tangent vector
, then the tangent vector 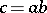 at
at  to the path
to the path 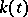 , where
, where
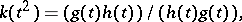 |
where 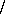 stands for right division, is a bilinear function of the vectors
stands for right division, is a bilinear function of the vectors  and
and 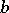 . The tangent space
. The tangent space 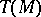 at
at  with the operation of multiplication
with the operation of multiplication 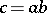 is called the tangent algebra of the loop
is called the tangent algebra of the loop 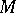 . In some neighbourhood
. In some neighbourhood 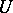 of the element
of the element 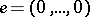 the coordinates
the coordinates 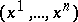 are said to be canonical of the first kind if for any vector
are said to be canonical of the first kind if for any vector 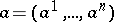 the curve
the curve 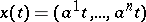 is a local one-parameter subgroup
is a local one-parameter subgroup 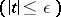 with tangent vector
with tangent vector  at
at  (see [1]). A power-associative analytic loop (cf. Algebra with associative powers) has canonical coordinates of the first kind [2]. In this case the mapping
(see [1]). A power-associative analytic loop (cf. Algebra with associative powers) has canonical coordinates of the first kind [2]. In this case the mapping 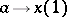 , defined for sufficiently small
, defined for sufficiently small  , makes it possible to identify
, makes it possible to identify 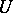 with a neighbourhood of the origin in
with a neighbourhood of the origin in 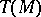 and to endow
and to endow 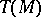 with the structure of a local analytic loop
with the structure of a local analytic loop 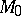 . If an analytic loop
. If an analytic loop  is alternative, that is, if any two elements of it generate a subgroup, then the tangent algebra
is alternative, that is, if any two elements of it generate a subgroup, then the tangent algebra 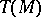 is a binary Lie algebra, and the multiplication
is a binary Lie algebra, and the multiplication 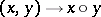 in
in 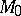 can be expressed by the Campbell–Hausdorff formula. Any finite-dimensional binary Lie algebra over the field
can be expressed by the Campbell–Hausdorff formula. Any finite-dimensional binary Lie algebra over the field 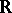 is the tangent algebra of one and only one (up to local isomorphisms) local alternative analytic loop [1].
is the tangent algebra of one and only one (up to local isomorphisms) local alternative analytic loop [1].
The most fully studied are analytic Moufang loops (cf. Moufang loop). The tangent algebra of an analytic Moufang loop satisfies the identities
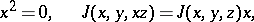 |
where
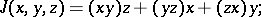 |
such algebras are called Mal'tsev algebras. Conversely, any finite-dimensional Mal'tsev algebra over 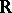 is the tangent algebra of a simply-connected analytic Moufang loop
is the tangent algebra of a simply-connected analytic Moufang loop 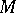 , defined uniquely up to an isomorphism (see [2], [3]). If
, defined uniquely up to an isomorphism (see [2], [3]). If 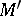 is a connected analytic Moufang loop with the same tangent algebra, and hence is locally isomorphic to
is a connected analytic Moufang loop with the same tangent algebra, and hence is locally isomorphic to 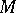 , then there is an epimorphism
, then there is an epimorphism 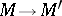 whose kernel
whose kernel 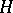 is a discrete normal subgroup of
is a discrete normal subgroup of 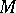 ; the fundamental group
; the fundamental group 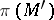 of the space
of the space 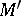 is isomorphic to
is isomorphic to 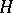 . If
. If 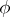 is a local homomorphism of a simply-connected analytic Moufang loop
is a local homomorphism of a simply-connected analytic Moufang loop 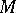 into a connected analytic Moufang loop
into a connected analytic Moufang loop 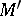 , then
, then 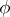 can be uniquely extended to a homomorphism of
can be uniquely extended to a homomorphism of 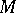 into
into 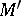 . The space of a simply-connected analytic Moufang loop with solvable Mal'tsev tangent algebra is analytically isomorphic to the Euclidean space
. The space of a simply-connected analytic Moufang loop with solvable Mal'tsev tangent algebra is analytically isomorphic to the Euclidean space 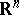 (see [3]).
(see [3]).
References
| [1] | A.I. Mal'tsev, "Analytic loops" Mat. Sb. , 36 : 3 (1955) pp. 569–578 (In Russian) |
| [2] | E.N. Kuz'min, "On the relation between Mal'tsev algebras and analytic Moufang loops" Algebra and Logic , 10 : 1 (1971) pp. 1–14 Algebra i Logika , 10 : 1 (1971) pp. 3–22 |
| [3] | F.S. Kerdman, "On global analytic Moufang loops" Soviet Math. Dokl. , 20 (1979) pp. 1297–1300 Dokl. Akad. Nauk SSSR , 249 : 3 (1979) pp. 533–536 |
Comments
References
| [a1] | O. Chein (ed.) H. Pflugfelder (ed.) J.D.H. Smith (ed.) , Theory and application of quasigroups and loops , Heldermann (1989) |
Loop, analytic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Loop,_analytic&oldid=11829